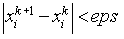Задача состоит в решении системы линейных уравнений вида:

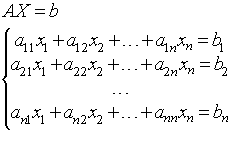
Матрица А размера (NxN) невырожденная. Для решения используется итеративный метод Якоби. Для этого исходная система заменяется эквивалентной:

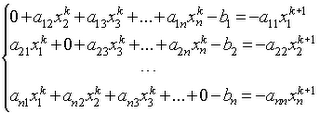
В начале делается некоторое начальное предположение X0, обычно равное вектору B=[b1/a11, ... ,bi/aii, ... ,bn/ann], т.е. Х0=В; затем метод генерирует на каждом шаге последовательность аппроксимаций Xk , k=1,2,3,... Для их вычисления используется следующая итеративная формула:

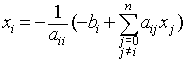
В общем случае итерации могут не сходится, тем не менее если система строго диагонально доминирующая то итерации будут сходится. Критерием окончания итерационного процесса может являться следующая проверка: