Алгоритм сортировки пузырьком:
Последовательный алгоритм пузырьковой сортировки (см., например, Кнут (1981), Кормен, Лейзерсон и Ривест (1999)) сравнивает и обменивает соседние элементы в последовательности, которую нужно отсортировать. Для последовательности:
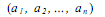
алгоритм сначала выполняет n-1 базовых операций "сравнения-обмена" для последовательных пар элементов:
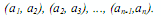
В результате после первой итерации алгоритма самый большой элемент перемещается ("всплывает") в конец последовательности. Далее последний элемент в преобразованной последовательности может быть исключен из рассмотрения, и описанная выше процедура применяется к оставшейся части последовательности:
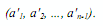
Как можно увидеть, последовательность будет отсортирована после n-1 итерации. Эффективность пузырьковой сортировки может быть улучшена, если завершать алгоритм в случае отсутствия каких-либо изменений сортируемой последовательности данных в ходе какой-либо итерации сортировки.

Алгоритм чет - нечетной перестановки:
Алгоритм пузырьковой сортировки в прямом виде достаточно сложен для распараллеливания – сравнение пар значений упорядочиваемого набора данных происходит строго последовательно. В связи с этим для параллельного применения используется не сам этот алгоритм, а его модификация, известная в литературе как метод чет-нечетной перестановки (odd-even transposition) – см., например, Kumar et al. (2003). Суть модификации состоит в том, что в алгоритм сортировки вводятся два разных правила выполнения итераций метода – в зависимости от четности или нечетности номера итерации сортировки для обработки выбираются элементы с четными или нечетными индексами соответственно, сравнение выделяемых значений всегда осуществляется с их правыми соседними элементами. Таким образом, на всех нечетных итерациях сравниваются пары:
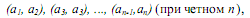
а на четных итерациях обрабатываются элементы:
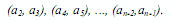
После n - кратного повторения итераций сортировки исходный набор данных оказывается упорядоченным.

Алгоритм быстрой сортировки:
При общем рассмотрении алгоритма быстрой сортировки, предложенной Хоаром (Hoare C.A.R.), прежде всего следует отметить, что этот метод основывается на последовательном разделении сортируемого набора данных на блоки меньшего размера таким образом, что между значениями разных блоков обеспечивается отношение упорядоченности (для любой пары блоков все значения одного из этих блоков не превышают значений другого блока). На первой итерации метода осуществляется деление исходного набора данных на первые две части – для организации такого деления выбирается некоторый ведущий элемент и все значения набора, меньшие ведущего элемента, переносятся в первый формируемый блок, все остальные значения образуют второй блок набора. На второй итерации сортировки описанные правила применяются рекурсивно для обоих сформированных блоков и т.д. При надлежащем выборе ведущих элементов после выполнения log2n итераций исходный массив данных оказывается упорядоченным.
Эффективность быстрой сортировки в значительной степени определяется правильностью выбора ведущих элементов при формировании блоков. В худшем случае трудоемкость метода имеет тот же порядок сложности, что и пузырьковая сортировка (т.е. T1~n2). При оптимальном выборе ведущих элементов, когда разделение каждого блока происходит на равные по размеру части, трудоемкость алгоритма совпадает с быстродействием наиболее эффективных способов сортировки (T1~nlog2n). В среднем случае количество операций, выполняемых алгоритмом быстрой сортировки, определяется выражением:
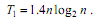
Общая схема алгоритма быстрой сортировки может быть представлена в следующем виде (в качестве ведущего элемента выбирается первый элемент упорядочиваемого набора данных):




