Анализ эффективности алгоритма сортировки пузырьком:

При анализе эффективности вначале проведем общую оценку сложности рассмотренного параллельного алгоритма сортировки, а затем дополним полученные соотношения показателями трудоемкости выполняемых коммуникационных операций.

Определим первоначально трудоемкость последовательных вычислений. При рассмотрении данного вопроса алгоритм пузырьковой сортировки позволяет продемонстрировать следующий важный момент. Как уже отмечалось в начале данного раздела, использованный для распараллеливания последовательный метод упорядочивания данных характеризуется квадратичной зависимостью сложности от числа упорядочиваемых данных:

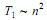
Однако применение подобной оценки сложности последовательного алгоритма приведет к искажению исходного целевого назначения критериев качества параллельных вычислений – показатели эффективности в этом случае будут характеризовать используемый способ параллельного выполнения данного конкретного метода сортировки, а не результативность использования параллелизма для задачи упорядочивания данных в целом как таковой. Различие состоит в том, что для сортировки могут быть применены более эффективные последовательные алгоритмы, трудоемкость которых имеет порядок:

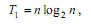
и для сравнения, насколько быстрее могут быть упорядочены данные при использовании параллельных вычислений, в обязательном порядке должна использоваться именно данная оценка сложности. Как основной результат выполненных рассуждений, можно сформулировать утверждение о том, что при определении показателей ускорения и эффективности параллельных вычислений в качестве оценки сложности последовательного способа решения рассматриваемой задачи следует использовать трудоемкость наилучших последовательных алгоритмов. Параллельные методы решения задач должны сравниваться с наиболее быстродействующими последовательными способами вычислений!

Определим теперь сложность рассмотренного параллельного алгоритма упорядочивания данных. Как отмечалось ранее, на начальной стадии работы метода каждый процессор проводит упорядочивание своих блоков данных (размер блоков при равномерном распределении данных является равным n/p). Предположим, что данная начальная сортировка может быть выполнена при помощи быстродействующих алгоритмов упорядочивания данных, тогда трудоемкость начальной стадии вычислений можно определить выражением вида:

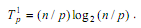
Далее на каждой выполняемой итерации параллельной сортировки взаимодействующие пары процессоров осуществляют передачу блоков между собой, после чего получаемые на каждом процессоре пары блоков объединяются при помощи процедуры слияния. Общее количество итераций не превышает величины p, и, как результат, общее количество операций этой части параллельных вычислений оказывается равным:

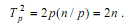
С учетом полученных соотношений показатели эффективности и ускорения параллельного метода сортировки имеют вид:

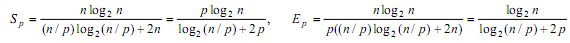
Расширим приведенные выражения – учтем длительность выполняемых вычислительных операций и оценим трудоемкость операции передачи блоков между процессорами. При использовании модели Хокни общее время всех выполняемых в ходе сортировки операций передачи блоков можно оценить при помощи соотношения вида:

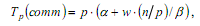
где α – латентность, β – пропускная способность сети передачи данных, а w есть размер элемента упорядочиваемых данных в байтах.

С учетом трудоемкости коммуникационных действий общее время выполнения параллельного алгоритма сортировки определяется следующим выражением:

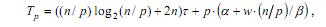
где τ есть время выполнения базовой операции сортировки.

Анализ эффективности алгоритма быстрой сортировки:

Оценим трудоемкость рассмотренного параллельного метода. Пусть у нас имеется N - мерный гиперкуб состоящий из p=2^N процессоров, где p < n.

Эффективность параллельного метода быстрой сортировки, как и в последовательном варианте, во многом зависит от правильности выбора значений ведущих элементов. Определение общего правила для выбора этих значений представляется затруднительным. Сложность такого выбора может быть снижена, если выполнить упорядочение локальных блоков процессоров перед началом сортировки и обеспечить однородное распределение сортируемых данных между процессорами вычислительной системы.

Определим вначале вычислительную сложность алгоритма сортировки. На каждой из log_p2 итераций сортировки каждый процессор осуществляет деление блока относительно ведущего элемента, сложность этой операции составляет n/p операций (будем предполагать, что на каждой итерации сортировки каждый блок делится на равные по размеру части).

При завершении вычислений процессоры выполняет сортировку своих блоков, что может быть выполнено при использовании быстрых алгоритмов за (n/p)log₂(n/p) операций.

Таким образом, общее время вычислений параллельного алгоритма быстрой сортировки составляет:

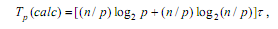
где τ есть время выполнения базовой операции перестановки.

Рассмотрим теперь сложность выполняемых коммуникационных операций. Общее количество межпроцессорных обменов для рассылки ведущего элемента на N-мерном гиперкубе может быть ограничено оценкой:

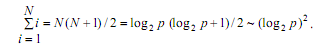
При используемых предположениях (выбор ведущих элементов осуществляется самым наилучшим образом), количество итераций алгоритма равно log₂p, а объем передаваемых данных между процессорами всегда является равным половине блока, т.е. (n/p)/2). При таких условиях, коммуникационная сложность параллельного алгоритма быстрой сортировки определяется при помощи соотношения:

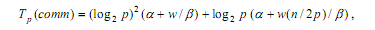
где α - латентность, β - пропускная способность сети, а w есть размер элемента набора в байтах.

С учетом всех полученных соотношений общая трудоемкость алгоритма оказывается равной: