|
|
 |
 Отчет
Постановка задачи
Целью данной работы является разработка программы, вычисляющей произведение квадратных матриц больших размерностей. Используя несколько потоков обработки данных, требуется разработать алгоритм, позволяющий достаточно ускорить этот процесс. За основу берется блочный алгоритм умножения матриц Фокса. Требуется провести сравнение работы алгоритма при использовании одного и двух потоков обработки данных.
Описание алгоритма и метод решения
Алгоритм Фокса
Итак, за основу параллельных вычислений для матричного
умножения при блочном разделении данных принят подход, при
котором базовые подзадачи отвечают за вычисления отдельных блоков
матрицы C и при этом в подзадачах на каждой итерации расчетов
располагается только по одному блоку исходных матриц A и B. Для
нумерации подзадач будем использовать индексы размещаемых в
подзадачах блоков матрицы C, т.е. подзадача (i,j) отвечает за
вычисление блока C ij – тем самым, набор подзадач образует
квадратную решетку, соответствующую структуре блочного
представления матрицы C. Возможный способ организации вычислений при таких условиях
состоит в применении широко известного алгоритма Фокса (Fox).
. В соответствии с алгоритмом Фокса в ходе вычислений на каждой
базовой подзадаче (i,j) располагается четыре матричных блока: - блок Cij матрицы C, вычисляемый подзадачей;
- блок Aij матрицы A, размещаемый в подзадаче перед началом вычислений;
- блоки A'ij, B'ij матриц A и B, получаемые подзадачей в ходе выполнения вычислений.
Выполнение параллельного метода включает: - этап инициализации, на котором каждой подзадаче (i,j)
передаются блоки Aij, Bij и обнуляются блоки Cij на всех
подзадачах;
- этап вычислений, в рамках которого на каждой итерации l, 0<=l< q, осуществляются следующие операции:
- для каждой строки i, 0<=i< q, блок Aij подзадачи (i,j)
пересылается на все подзадачи той же строки i решетки; индекс j,
определяющий положение подзадачи в строке, вычисляется в
соответствии с выражением j = ( i + l ) mod q
где mod есть операция получения остатка от целочисленного деления; - полученные в результаты пересылок блоки A'ij, B'ij каждой
подзадачи (i, j) перемножаются и прибавляются к блоку Cij
- блоки >B'ij каждой подзадачи (i,j) пересылаются подзадачам,
являющимся соседями сверху в столбцах решетки подзадач (блоки
подзадач из первой строки решетки пересылаются подзадачам
последней строки решетки).
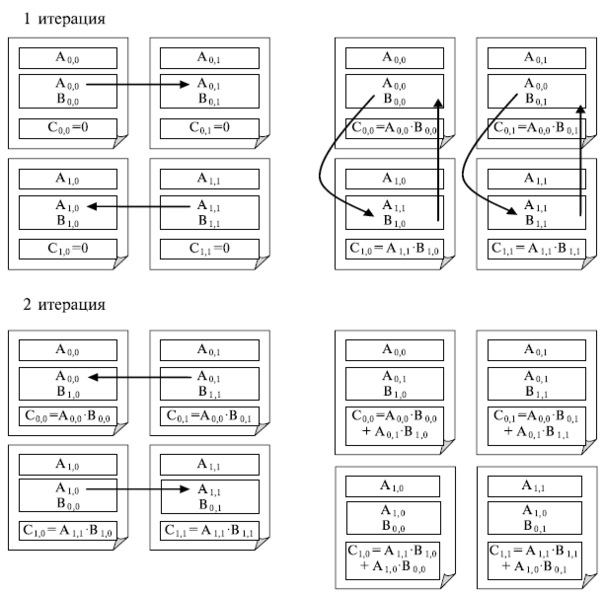
Для пояснения этих правил параллельного метода на рис. 7.6
приведено состояние блоков в каждой подзадаче в ходе выполнения
итераций этапа вычислений (для решетки подзадач 2x2 ).
Оценка эффективности
Определим вычислительную сложность данного алгоритма Фокса.
Построение оценок будет происходить при условии выполнения всех
ранее выдвинутых предположений: все матрицы являются квадратными
размера nxn, количество блоков по горизонтали и вертикали
являются одинаковым и равным q (т.е. размер всех блоков равен kxk, k=n/q ), процессоры образуют квадратную решетку и их
количество равно p=q 2.Как уже отмечалось, алгоритм Фокса требует для своего
выполнения q итераций, в ходе которых каждый процессор
перемножает свои текущие блоки матриц А и В и прибавляет
результаты умножения к текущему значению блока матрицы C.
Примем за Ts - время работы последовательного алгоритма, за Tp - время работы параллельного алгоритма, за S - ускорение, за E - эффективность, за p – количество процессоров.
При применении последовательного алгоритма перемножения матриц число шагов имеет порядок O(n3).
С
учетом выдвинутых предположений общее количество выполняемых при
этом операций будет иметь порядок n3/p. Как результат, показатели
ускорения и эффективности алгоритма имеют вид:
Sp = n3 / ( n3 / p) = p
Ep = n3 / [ p * ( n3 / p) ] = 1
|
Общий анализ сложности снова дает идеальные показатели
эффективности параллельных вычислений. Уточним полученные
соотношения — для этого укажем более точно количество
вычислительных операций алгоритма и учтем затраты на выполнение операций передачи данных между процессорами.Определим количество вычислительных операций. Сложность
выполнения скалярного умножения строки блока матрицы A на столбец
блока матрицы В можно оценить как 2(n/q)-1. Количество строк и
столбцов в блоках равно n/q и, как результат, трудоемкость
операции блочного умножения оказывается равной (n2/p)(2n/q-1).
Для сложения блоков требуется n2/p операций. С учетом всех
перечисленных выражений время выполнения вычислительных операций
алгоритма Фокса может быть оценено следующим образом:
Tp(calc) = q * ( n2 / p ) * ( 2 n - 1 ) * t,
(напомним, что t есть время выполнения одной элементарной скалярной операции).Оценим затраты на выполнение операций передачи данных между
процессорами. На каждой итерации алгоритма перед умножением
блоков один из процессоров строки процессорной решетки рассылает
свой блок матрицы A остальным процессорам своей строки. Как уже
отмечалось ранее, при топологии сети в виде гиперкуба или полного
графа выполнение этой операции может быть обеспечено за log2q
шагов, а объем передаваемых блоков равен n2/p. Как результат,
время выполнения операции передачи блоков матрицы A при
использовании модели Хокни может оцениваться как
T1p(comm) = log 2 q ( a + w( n2 / p ) / b),
где a – латентность, b – пропускная способность сети
передачи данных, а w есть размер элемента матрицы в байтах. В
случае же когда топология строк процессорной решетки представляет
собой кольцо, выражение для оценки времени передачи блоков
матрицы A принимает вид:
T'1p(comm) = (q / 2)( a + w( n2 / p ) / b),
Далее после умножения матричных блоков процессоры передают
свои блоки матрицы В предыдущим процессорам по столбцам
процессорной решетки (первые процессоры столбцов передают свои
данные последним процессорам в столбцах решетки). Эти операции
могут быть выполнены процессорами параллельно, и, тем самым,
длительность такой коммуникационной операции составляет:
T - p2(comm) = a + w( n2 / p ) / b),
Просуммировав все полученные выражения, можно получить, что
общее время выполнения алгоритма Фокса может быть определено при
помощи следующих соотношений:
Tp(calc) = q *[ ( n2 / p ) * ( 2 n/ q - 1 ) + ( n2 / p )] * t + q*log 2 q ( a + w( n2 / p ) / b) + (q - 1)* ( a + w( n2 / p ) / b) =
q *[ ( n2 / p ) * ( 2 n/ q - 1 ) + ( n2 / p )] * t + (q*log 2 q + (q - 1)) ( a + w( n2 / p ) / b) ,
(напомним, что параметр q определяет размер процессорной решетки
и q = sqrt (p).
Демонстрация
Алгоритм Фокса.

Результаты вычислительных экспериментов
Эксперименты проводились на двухпроцессорном вычислительном узле на базе двухядерных процессоров Intel® CoreTM2 Duo P8400 (2.26ГГц)
| Размер матрицы | Последовательное умножение(сек) | Парпллельное умножение 4 процесса(сек) | Ускорение |
| 200 | 0.160467 | 2.309030 | 0.069495 |
| 400 | 1.031636 | 3.457076 | 0.298413 |
| 600 | 6.397268 | 4.765645 | 1.342372 |
| 800 | 15.696137 | 9.581551 | 1.638163 |
| 1000 | 35.410325 | 16.658564 | 2.125653 |
| 1400 | 57.279282 | 42.035280 | 1.362648 |
| 1500 | 70.878405 | 52.293270 | 1.355402 |
|



