Постановка задачи
Одной из основных задач обработки данных является сортировка. Алгоритм сортировки — это алгоритм для упорядочения элементов в списке.
Пусть дана последовательность чисел
a[1], a[2],…,a[n], n>1.
Необходимо упорядочить ее элементы таким образом, чтобы для любых i,j : 1<=i a[i]<=a[j].
В случае, когда количество элементов последовательности достаточно велико в целях уменьшения времени обработки данных, возможно использование параллельных вычислений. При этом необходимо модифицировать уже имеющиеся последовательные или разработать новые параллельные алгоритмы сортировки. В лабораторной работе рассмотрен алгоритм быстрой сортировки и его параллельный вариант, написанный с использованием библиотеки MPI.
Метод решения
Последовательный алгоритм
Последовательный алгоритм быстрой сортировки основан на операции последовательного разделения сортируемого набора данных на блоки меньшего размера таким образом, что между значениями разных блоков обеспечивается отношение упорядоченности: для любых двух блоков найдётся блок, все значения которого меньше значений второго блока.
На первой итерации метода производится деление исходной последовательности данных на первые две части - для осуществления этого деления в последовательности выбирается некоторый ведущий элемент и все значения набора, меньшие ведущего элемента или равные ему, переносятся в первый формируемый блок, все остальные значения составляют второй блок последовательности. На последующих итерациях сортировки описанная выше схема применяется последовательно для каждого из вновь сформированных блоков. После выполнения log n (n - число элементов исходной последовательности) итераций исходный массив будет упорядочен.
Эффективность быстрой сортировки в значительной степени определяется правильностью выбора ведущих элементов при формировании блоков. В худшем случае трудоемкость метода имеет тот же порядок сложности, что и пузырьковая сортировка (т.е. T1~n2 ). При оптимальном выборе ведущих элементов, когда разделение каждого блока происходит на равные по размеру части, трудоемкость алгоритма оценивается как nlog(n).
Параллельный алгоритм
Параллельное обобщение алгоритма быстрой сортировки наиболее простым способом может быть получено, если топология коммуникационной сети может быть эффективно представлена в виде N -мерного гиперкуба (т.е. p=2^N ). Пусть исходный набор данных распределен между процессорами блоками одинакового размера n/p ; результирующее расположение блоков должно соответствовать нумерации процессоров гиперкуба.
Предполагается, что вначале каждый процессор имеет часть исходных данных для сортировки.
Сортировка располагаемых на процессорах блоков происходит в самом начале выполнения вычислений. Для поддержки упорядоченности в ходе вычислений процессоры должны выполнять операции слияния частей блоков, получаемых после разделения.
После окончания параллельного алгоритма сортировки каждый процессор будет содержать некоторую часть отсортированного массива так, что:
1) Каждая часть отсортирована
2) Для всех i
Для N -мерного гиперкуба алгоритм можно представить в следующем виде:
1) для i=N до 1
1.1) для каждого i-мерного куба
ведущий процессор рассылает его средний элемент всем в i-кубе в качестве ведущего элемента (pivot)
1.2) выделяем для (i-1)-куба в этом i-кубе
1.3) каждая пара процессоров-партнеров в (i-1)-кубе обменивается данными:
процессор с меньшим номером отдает партнеру элементы больше ведущего
процессор с большим номером отдает партнеру элементы меньше ведущего
на каждом из процессоров происходит слияние данных
Заметим, что на i-ой итерации, каждый из подгиперкубов будут образовывать процессоры, в битовых представлениях номеров которых различаются i-ые (слева) позиции;
После первой итерации все элементы в нижнем (N-1)-мерном кубе будут меньше, чем все элементы в верхнем (N-1)-мерном кубе. После N таких шагов массив будет отсортирован.
Анализ эффективности
Cложность алгоритма сортировки
После разделения исходного набора данных, каждый процессор выполняет разбиение своего блока на два, согласно ведущему элементу. Это может быть выполнено за n/p операций (будем предполагать, что на каждой итерации сортировки каждый блок делится на равные по размеру части). Также, на каждой из итераций, каждый процессор выполняет слияние частей блоков, сложность этой операции оценивается величиной (n/p). После всех итераций, мы выполняем последовательную операцию быстрой сортировки.
Таким образом, общее время вычислений параллельного алгоритма быстрой сортировки оценивается величиной:
[2(n/p)(log₂p) + (n/p)log₂ (n/p)]*t,
где t - время выполнения базовой операции перестановки.
Сложность выполняемых коммуникационных операций
Общее количество межпроцессорных обменов для рассылки ведущего элемента на N-мерном гиперкубе может быть ограничено оценкой (log₂p)^2. При используемых предположениях (выбор ведущих элементов осуществляется самым наилучшим образом, количество итераций алгоритма равно (log₂p), а объем передаваемых данных между процессорами всегда является равным половине блока, т.е. (n/p)/2),
коммуникационная сложность параллельного алгоритма быстрой сортировки определяется при помощи соотношения
(α+w/β)(log₂p)^2 + (α+w(n/2p)/β)(log₂p),
где α - латентность, β - пропускная способность сети, а w – размер элемента набора в байтах.
Общая трудоемкость алгоритма
С учетом полученных соотношений, она равна
[2(n/p)(log₂p) + (n/p)log₂(n/p)]*t + (α+w/β)(log₂p)^2 + (α+w(n/2p)/β)(log₂p).
При этом, время коммуникаций определяется в основном временем передачи данных.
Результаты вычислительных экспериментов
Конфигурация оборудования:
AMD Athlon 64 X2 Dual Core processor 5000+ 2.60 GHz
Cache: L1 64Kb per core L2 512Kb per core
RAM: 4,5Gb DDR2
Compiler: MS Visual Studio 2010
Результаты измерений при запуске двух процессов:
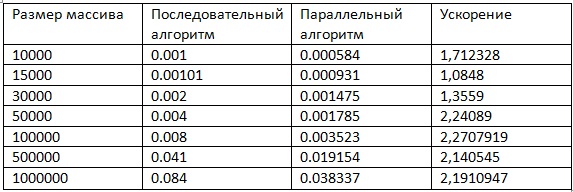
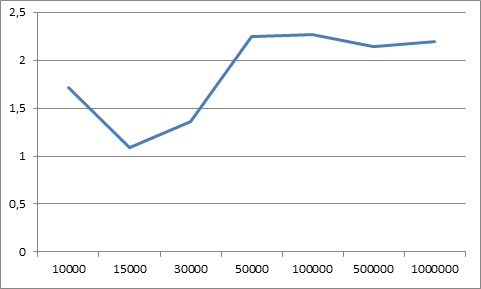
Результаты экспериментов можно увидеть на графике:
Демонстрация
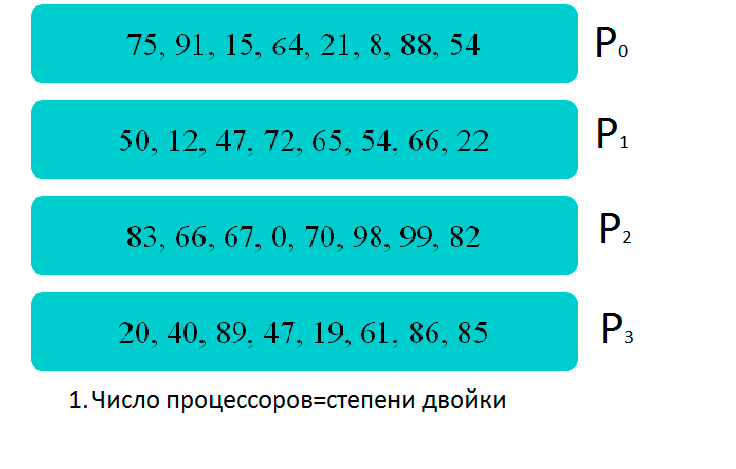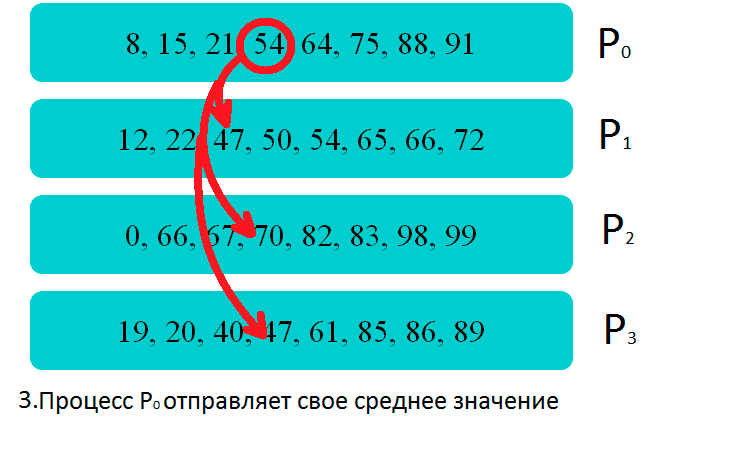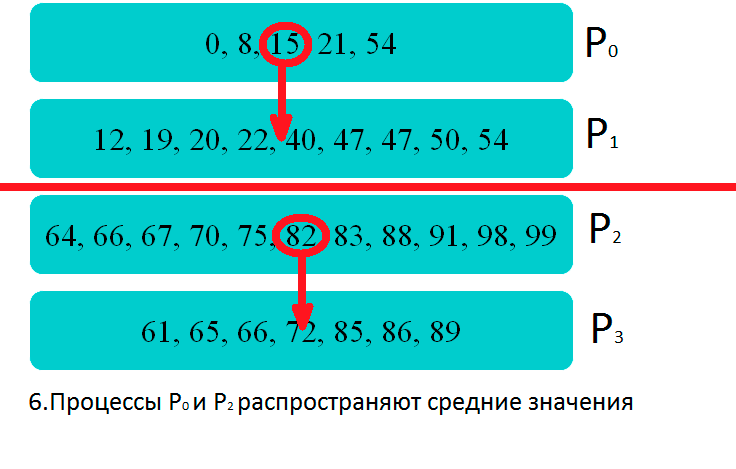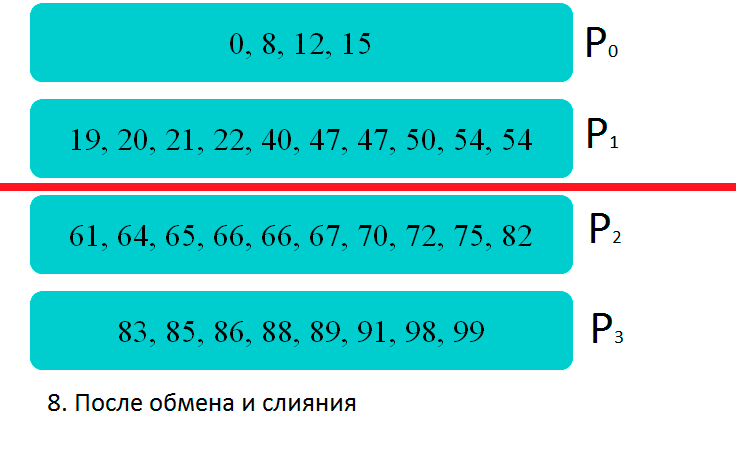
Демонстрация работы параллельного алгоритма на четырех процессорах:
Об авторах
Работу выполнила:
студентка группы 8409 Борисова А.Ю.
| 


