Постановка задачи

Пусть дан произвольный массив

или любому другому множеству с введённым отношением порядка. Требуется упорядочить элементы этого массива таким образом, чтобы

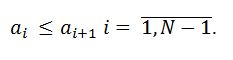
Решение данной задачи за малое время является очень важным, так как именно отсортированные массивы используются во многих алгоритмах. Например, если массив отсортирован, то производить поиск в нём можно за гораздо меньшее время, если использовать двоичный поиск вместо поэлементного просмотра. Известно много алгоритмов сортировки массивов, которые отличаются использованием дополнительной памяти, а также оценками эффективности выполнения в зависимости от размера входных данных. Наилучшим по быстродействию на практике считается алгоритм быстрой сортировки. Этот алгоритм использует принцип «разделяй и властвуй», а, следовательно, он успешно может быть распараллелен. Цель данной работы – рассмотреть один из вариантов распараллеливания алгоритма быстрой сортировки, который использует идею представления процессов как узлов гиперкуба, изучить анализ его эффективности и определить ускорение параллельного алгоритма при выполнении на нескольких процессорах. Для реализации приложения, выполняющегося с использованием множества процессов будем использовать библиотеку MPI.

Описание последовательного алгоритма

• Выбираем в массиве некоторый элемент, который будем называть опорным элементом. С точки зрения корректности алгоритма выбор опорного элемента безразличен

• Операция разделения массива: реорганизуем массив таким образом, чтобы все элементы, меньшие или равные опорному элементу, оказались слева от него, а все элементы, большие опорного — справа от него. Обычный алгоритм операции:

 o	Два индекса — l и r, приравниваются к минимальному и максимальному индексу разделяемого массива соответственно.

 o	Вычисляется индекс опорного элемента m. 

 o	Индекс l последовательно увеличивается до m до тех пор, пока l-й элемент не превысит опорный. 

 o	Индекс r последовательно уменьшается до m до тех пор, пока r-й элемент не окажется меньше либо равен опорному. 

 o	Если r = l — найдена середина массива — операция разделения закончена, оба индекса указывают на опорный элемент.

 o	Если l < r — найденную пару элементов нужно обменять местами и продолжить операцию разделения с тех значений l и r, которые были достигнуты.

Следует учесть, что если какая-либо граница (l или r) дошла до опорного элемента, то при обмене значение m изменяется на r-й или l-й элемент соответственно.

• Рекурсивно упорядочиваем подмассивы, лежащие слева и справа от опорного элемента.

• Базой рекурсии являются наборы, состоящие из одного или двух элементов. Первый возвращается в исходном виде, во втором, при необходимости, сортировка сводится к перестановке двух элементов.

Код последовательного алгоритма

Так как на каждом уровне рекурсии размер разделяемых частей уменьшается как минимум на единицу, то алгоритм точно остановится через конечное число шагов (уровней рекурсии)

Эффективность работы алгоритма во многом зависит от выбираемого опорного элемента. В самом худшем случае может возникнуть ситуация, при которой на каждой итерации массив разделяется так, что одна часть представляет собой единственный элемент, при этом выполняется O(n^2) операций, где n – длина сортируемого массива. Тем не менее, вероятность получения такой ситуации на каждой итерации очень мала. В идеальном случае, когда на каждой итерации массив разделяется на две одинаковые части, эффективность алгоритма равна

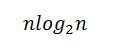
В среднем же случае количество операций метода быстрой сортировки равно

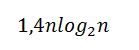
Следует отметить также, что одним из существенных недостатков этого алгоритма является то, что при больших n и неудачных выборах опорного элемента вложенность рекурсии составляется порядка O(n), что может привести к переполнению стека вызовов.

Описание параллельного алгоритма

Параллельное обобщение алгоритма быстрой сортировки наиболее простым способом может быть получено, если топология коммуникационной сети может быть эффективно представлена в виде N – мерного гиперкуба, т.е. когда p = 2^N, где p – число процессов. Тогда первая итерация алгоритма состоит в следующем:

o	В начале разделяем исходный массив из n элементов на p частей и рассылаем каждому процессу его часть. Сортируем её алгоритмом быстрой сортировки.
o	Выбираем каким-то образом опорный элемент. В нашей реализации алгоритма мы выбираем в качестве опорного средний элемент ведущего процесса.
        Рассылаем этот элемент по всем остальным процессам. Выбираемый подобным образом ведущий элемент в отдельных случаях может оказаться более близким к реальному среднему значению всего сортируемого набора,
        чем какое-либо другое произвольно выбранное значение.
o	Производим разделение данных каждого процесса на элементы, меньшие, либо равные значению опорного элемента и большие значения опорного.
o	Образуем пары процессов, для которых битовое представление номера отличается только в старшем бите (позиции N) и производим взаимообмен между этими процессами:
        процесс, который в данной позиции имеет бит, равный нулю, получает от другого часть элементов, меньших опорного и отдаёт часть своих элементов, 
        которые превышают опорный элемент. После передачи обе части сливаются с линейной от размера блока данных процесса сложностью.
        Т.о. на каждой итерации набор данных каждого процесса остаётся упорядоченным.

После первой итерации общий гиперкуб разобьётся на два под-гиперкуба, процессы одной части содержат элементы, меньшие, либо равные опорному (в битовой представлении номеров которых в позиции N стоит 0), а процессы другой части будут иметь элементы, большие опорного. Очевидно, общий гиперкуб из p процессоров, размерности N разбился на два под-куба по p/2 процессоров размерности N-1.

Описанная процедура далее применяется рекурсивно для двух полученных гиперкубов. Однако, теперь при реализации алгоритма нам не обязательно использовать рекурсию, мы можем придерживаться итеративной схемы: пары на каждой итерации i образуют процессы, чьи номера в битовом представлении отличаются только в позиции i.

На второй итерации оба гиперкуба снова распадутся на два, при этом новые опорные элементы выбираются как средние элементы каждого из ведущих процессов новых гиперкубов (они обладают наименьшим номером). Первый под-гиперкуб из четырёх будет содержать элементы, меньшие опорного на первой итерации и меньшие опорного элемента второй итерации для данного куба (он меньше, либо равен первому опорному элементу) и аналогично для других под-гиперкубов. Тогда очевидно, что после N итераций для получения упорядоченного массива нам лишь останется собрать отсортированные блоки данных с каждого процесса в порядке возрастания их номеров.

Демонстрация работы параллельного алгоритма

Пусть p = 4

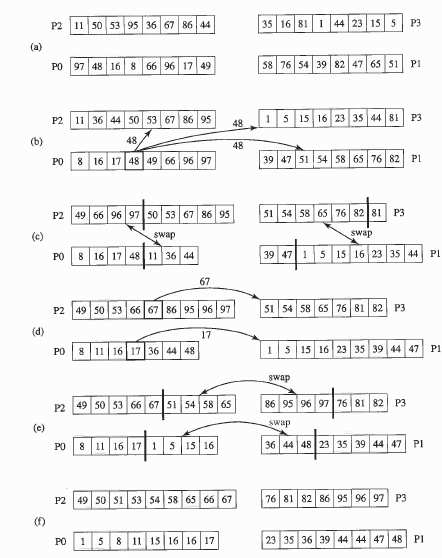
Оценка эффективности параллельного алгоритма

Дано: p процессоров p=2^N, n – размер сортируемого массива. N – известное нам число итераций параллельного алгоритма

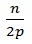
Вывод оценок эффективности будем производить в предположении о том, что на каждой итерации мы выбираем опорный элемент наиболее удачным способом и размер пересылаемых частей всегда одинаков и равен При этом размер блока данных каждого процесса на каждой итерации одинаков и равен

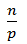
Итак, перед началом работы алгоритма каждый процессор выполняет сортировку своего блока данных. При использовании быстрой сортировки оценка числа операций 

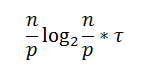
где т – время выполнения элементарной операции перестановки элементов в массиве.

На каждой из N = log2(p) итераций каждый процессор выполняет разделение своего блока данных по опорному элементу. Так как блок данных упорядочен, то это разделение можно провести путём поиска опорного элемента в этом блоке двоичным поиском, оценка числа операций для поиска:

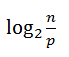
Также на каждой итерации происходит слияние двух блоков данных: оставшегося на процессоре и принятого от другого процессора. Как мы оговаривали выше, размеры обоих этих блоков равны по n/2p и, таким образом, оценка числа операций для процедуры слияния двух частей

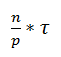
Так как обе эти операции выполняются на каждой из N = log2(p) итераций, то в общую оценку они входят с множителем N.

Таким образом, общее время вычислений параллельного алгоритма быстрой сортировки составляет:

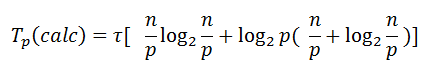
Теперь рассмотрим сложность выполняемых коммуникационных операций. Общее количество межпроцессных обменов для рассылки ведущего элемента на N-мерном гиперкубе может быть ограничено оценкой

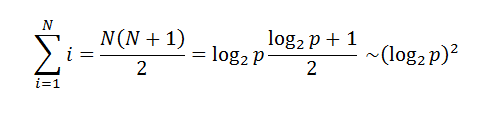
Кроме того, на каждой из N = log2(p) итераций происходит пересылка n/2p элементов между каждой парой процессов, тогда коммуникационная сложность параллельного алгоритма быстрой сортировки:

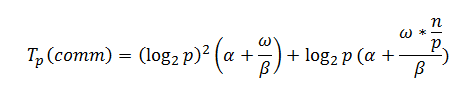
где alpha – латентность, beta – пропускная способность сети, omega – размер элементарного набора в байтах. Результирующая временная сложность алгоритма быстрой сортировки:

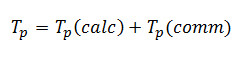
Результаты проведённых экспериментов

Информация о компьютере, на котором проводились эксперименты:
Процессор - Intel Core i7 2630QM @ 2.0 GHz with Hyper-Threading
Number of cores: 4
Threads: 8
L3 Cache 6 Mb
L2 Cache 1 Mb
RAM Size 6 Gb
OS Windows 7 x32
Compiler: MS Visual Studio 2010

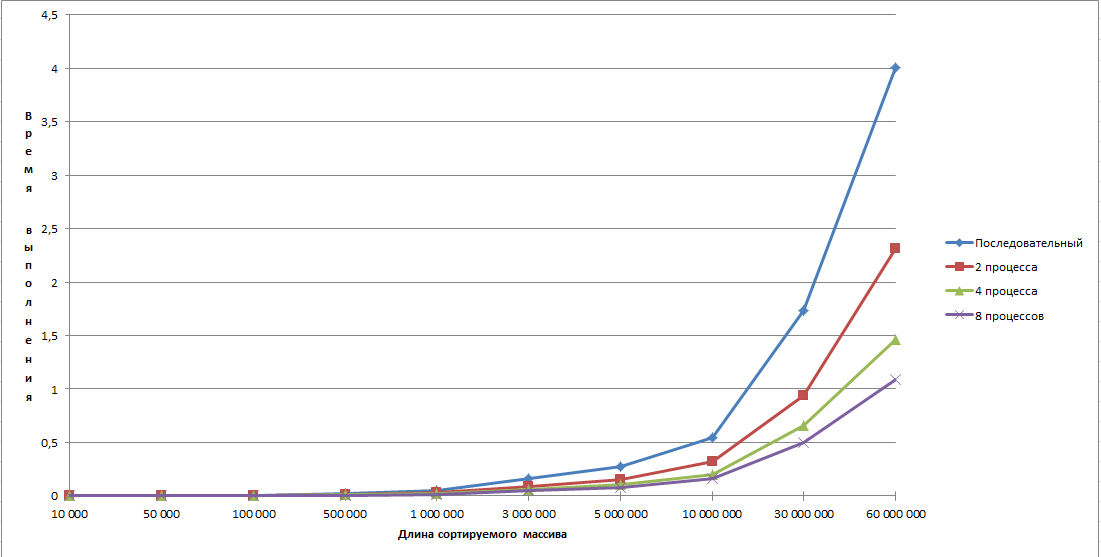
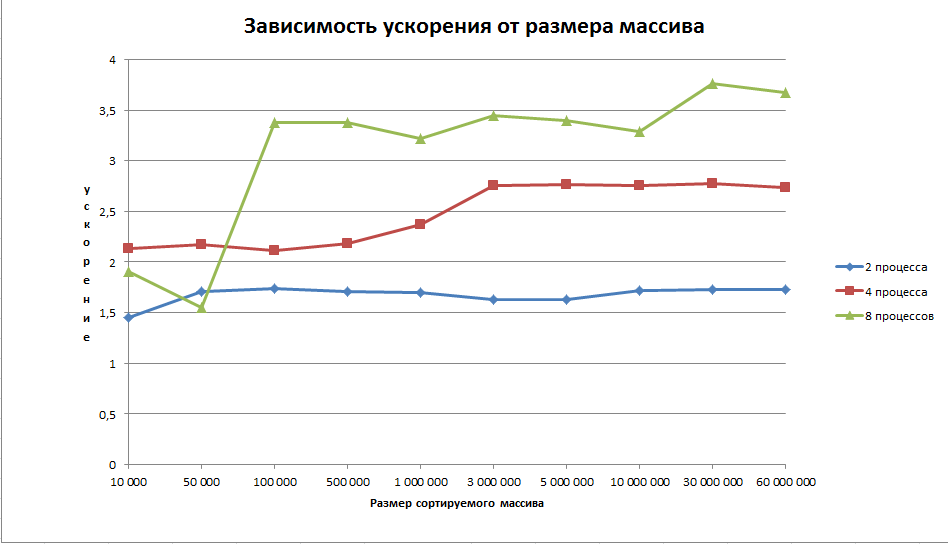
На графиках видно, что при сравнительно небольшом объёме данных ускорение на восьми процессах хуже, чем при двух или четырёх. Это связано с тем, что эффективнее отсортировать данные на имеющемся числе процессоров, чем тратиться на пересылку, тем не менее при возрастании числа процессов, мы уже получаем существенный выигрыш при использовании большого числа процессов.

Вывод

Итак, мы на практике убедились, что распараллеливание последовательного алгоритма быстрой сортировки даёт существенный выигрыш в производительности, так как каждый процессор сортирует меньшую часть элементов, чем сортирует один процессор в последовательном алгоритме. По той же причине параллельный алгоритм позволяет обойти опасность переполнения стека и мы можем сортировать массивы ещё большего размера.

Об авторе

Работу выполнил студент группы 8409, Галанов Дмитрий Сергеевич.