1) Реализовать последовательный алгоритм перемножения матриц.
2) Реализовать программу блочного умножения матриц (Алгоритм Фокса), используя технологию MPI.
3) Провести расчет теоретического ускорения и эффективности.
4) Провести ряд тестов. Сравнить ускорение параллельного и не параллельного алгоритма.
Используется блочная схема разбиения матрицы. При таком способе разделения данных исходные матрицы А, В и результирующая матрица С представляются в виде наборов блоков. Далее предполагается что все матрицы являются квадратными размера n×n, количество блоков по горизонтали и вертикали одинаково и равно q (т.е. размер всех блоков равен k×k, k=n/q). При таком представлении данных операция матричного умножения матриц А и B в блочном виде может быть представлена так:
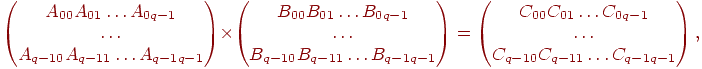
,где каждый блок результирующей матрицы С определяется по формуле
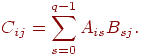
За основу параллельных вычислений для матричного умножения при блочном разделении данных принят подход, при котором базовые подзадачи отвечают за вычисления отдельных блоков матрицы C и при этом в подзадачах на каждой итерации расчетов располагается только по одному блоку исходных матриц A и B. Для нумерации подзадач будем использовать индексы размещаемых в подзадачах блоков матрицы C, т.е. подзадача (i,j) отвечает за вычисление блока Cij – тем самым, набор подзадач образует квадратную решетку, соответствующую структуре блочного представления матрицы C.
В соответствии с алгоритмом Фокса в ходе вычислений на каждой базовой подзадаче (i,j) располагается четыре матричных блока:
1. Блок Cij матрицы C, вычисляемый подзадачей;
2. Блок Aij матрицы A, размещаемый в подзадаче перед началом вычислений;
3. Блоки A'ij , B'ij матриц A и B, получаемые подзадачей в ходе выполнения вычислений.
Выполнение параллельного метода включает:
1. Этап инициализации, на котором каждой подзадаче (i,j) передаются блоки Aij, Bij и обнуляются блоки Cij на всех подзадачах;
2. Этап вычислений, в рамках которого на каждой итерации l, l от нуля (включительно) до q, осуществляются следующие операции:
a. Для каждой строки i (i от нуля включительно и строго до q) блок Aij подзадачи (i,j) пересылается на все подзадачи той же строки i решетки; индекс j, определяющий положение подзадачи в строке, вычисляется в соответствии с выражением j=(i+l)mod q, где mod есть операция получения остатка от целочисленного деления;
b. Полученные в результаты пересылок блоки A'ij, B'ij каждой подзадачи (i,j) перемножаются и прибавляются к блоку Cij
c. Блоки B'ij каждой подзадачи (i,j) пересылаются подзадачам, являющимся соседями сверху в столбцах решетки подзадач (блоки подзадач из первой строки решетки пересылаются подзадачам последней строки решетки).
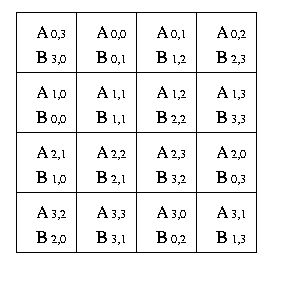
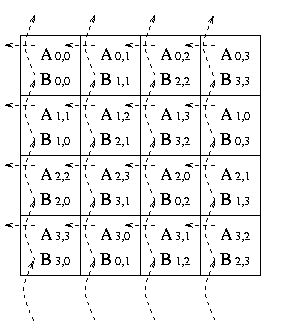
Изначально блоки матриц-операндов A и B располагаются следующим образом:
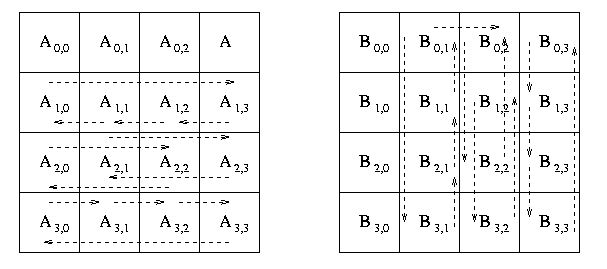
После первой итерации вычислений перемножены были следующие блоки матриц A и B:
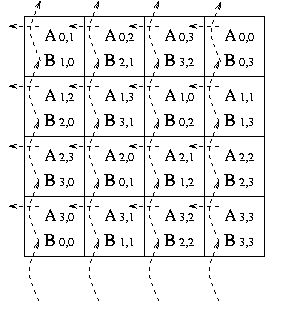
После первого сдвига перемножены будут следующие блоки матриц A и B:
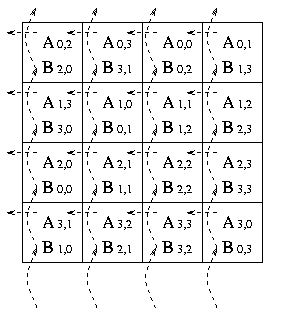
После второго сдвига перемножены будут следующие блоки матриц A и B:
После третьего сдвига перемножены будут следующие блоки матриц A и B: