Постановка задачи

Пусть G есть граф G = (RV), для которого набор вершин νi, 1≤ i ≤n, задается множеством V, а список ребер графа rj = (vsj,vtj), 1≤j≤m определяется множеством R. Ребрам графа приписаны некоторые числовые характеристики (веса) wj, 1≤j≤m. Граф полагаем ориентированным. Для имеющегося графа G требуется найти минимальные длины путей между каждой парой вершин графа. В качестве практического примера можно привести задачу составления оптимального маршрута движения транспорта между различными городами при заданном расстоянии между населенными пунктами. Вершинами графа в этой задаче моделируются города, рёбрами — соединяющие их дороги. Веса рёбер графа определяют расстояния между городами.

Графы задаются при помощи матрицы смежности. Элемент матрицы характеризует вес ребра, входящего в вершину. На главной диагонали матрицы стоят нули. Для обозначения отсутствия ребра между вершинами при вычислениях используется -1. Использование матрицы смежности позволяет применять при реализации вычислительных процедур анализа графов матричные алгоритмы обработки данных.

В данной работе разобран алгоритм Флойда для решения задачи поиска оптимальных путей на графе и произведена его последовательная и параллельная реализация.

Цели работы:

1) Реализовать последовательную версию алгоритма Флойда;

2) Реализовать параллельную версию алгоритма Флойда с помощью библиотеки MPI;

3) Оценить эффективность параллельной схемы и привести результаты вычислительных экспериментов.

Метод решения

Для поиска минимальных расстояний между всеми парами пунктов назначения Флойд предложил алгоритм, сложность которого имеет порядок O(n^3). В общем виде данный алгоритм может быть представлен следующим образом:

// Последовательный алгоритм Флойда

for (k = 0; k < n; k++)

for (i = 0; i < n; i++)

for (j = 0; j < n; j++)

A[i,j] = min(A[i,j],A[i,k]+A[k,j]);

Реализация операции выбора минимального значения min должна учитывать способ указания в матрице смежности несуществующих ребер графа. Как можно заметить, в ходе выполнения алгоритма матрица смежности A изменяется, после завершения вычислений в матрице A будет храниться требуемый результат – длины минимальных путей для каждой пары вершин исходного графа.

Параллельная схема

Как следует из общей схемы алгоритма Флойда, основная вычислительная нагрузка при решении задачи поиска кратчайших путей состоит в выполнении операции выбора минимального значения. Данная операция является достаточно простой и ее распараллеливание не приведет к заметному ускорению вычислений. Более эффективный способ организации параллельных вычислений может состоять в одновременном выполнении нескольких операций обновления значений матрицы A.

Покажем корректность такого способа организации параллелизма. Для этого нужно доказать, что операции обновления значений матрицы A на одной и той же итерации внешнего цикла k могут выполняться независимо. Иными словами, следует показать, что на итерации k не происходит изменения элементов Aik и Akj ни для одной пары индексов (i, j). Рассмотрим выражение, по которому происходит изменение элементов матрицы A:

Aij <- min (Aij, Aik + Akj).

Для i=k получим

Akj <- min (Akj, Akk + Akj),

но тогда значение Akj не изменится, т.к. Akk=0.

Для j=k выражение преобразуется к виду

Aik <- min (Aik, Aik + Akk),

что также показывает неизменность значений Aik. Как результат, необходимые условия для организации параллельных вычислений обеспечены, и, тем самым, в качестве базовой подзадачи может быть использована операция обновления элементов матрицы A (для указания подзадач будем применять индексы обновляемых в подзадачах элементов).

Выполнение вычислений в подзадачах становится возможным только тогда, когда каждая подзадача (i, j) содержит необходимые для расчетов элементы Aij, Aik, Akj матрицы A. Для исключения дублирования данных разместим в подзадаче (i, j) единственный элемент Aij, тогда получение всех остальных необходимых значений может быть обеспечено только при помощи передачи данных.

В работе использовалось горизонтальное разбиение матрицы, т.е. каждому процессу передавалось несколько строк матрицы, с которыми он выполнял необходимые действия.

Параллельный алгоритм Флойда заключается в том, что на k-й итерации мы отсылаем k-ю строку всем процессам, а затем каждый процесс выполняет последовательный алгоритм Флойда для своей полосы матрицы смежности, одновременно обновляя значение матрицы.

Анализ эффективности

Оценим порядок вычислительной сложности алгоритма.

Как было указано выше, общая трудоёмкость последовательного алгоритма Флойда O(n^3).

Для параллельного алгоритма на отдельной итерации каждый процессор выполняет обновление элементов матрицы A. Всего в подзадачах n^2/p таких элементов, число итераций алгоритма равно n, таким образом, показатели ускорения и эффективности параллельного алгоритма Флойда имеют вид (p – число процессоров):

Sp = n^3/(n^3/p) = p,

Ep = n^3/(p(n^3⁄p)) = 1.

Общий анализ сложности дает идеальные показатели эффективности параллельных вычислений.

Для параллельного выполнения алгоритма Флойда над графом, содержащим n вершин, требуется выполнение n итераций алгоритма, на каждой из которых параллельно выполняется обновление всех элементов матрицы смежности. Значит, время выполнения вычислений составляет:

Tp = n^2(n/p)τ,

где τ есть время выполнения операции выбора минимального значения, однако при этом не учтены коммуникационные операции.

Коммуникационная операция, выполняемая на каждой итерации алгоритма Флойда, состоит в передаче одной из строк матрицы A всем процессорам вычислительной системы. Выполнение такой операции может быть выполнено за log2 p шагов.

Общая длительность выполнения коммуникационных операций:

Tp(comm) = n log2 p (α + wn/β),

где α – латентность сети передачи данных, β – пропускная способность сети, w – размер элемента матрицы в байтах.

Общее время выполнения параллельного алгоритма Флойда:

Tp(общ) = n^3/p τ + n log2 p (α + wn/β).

Демонстрация

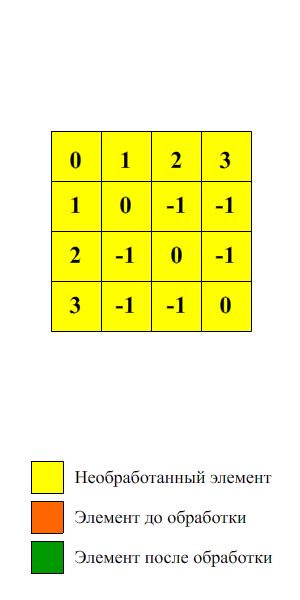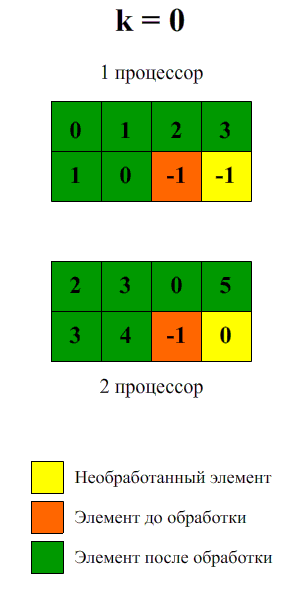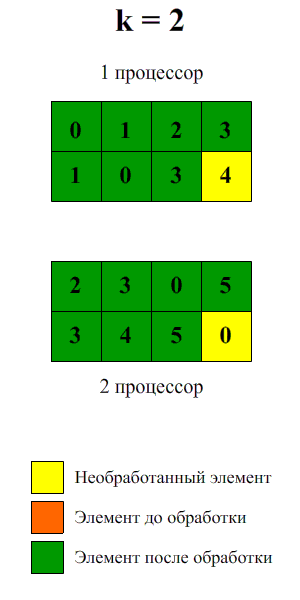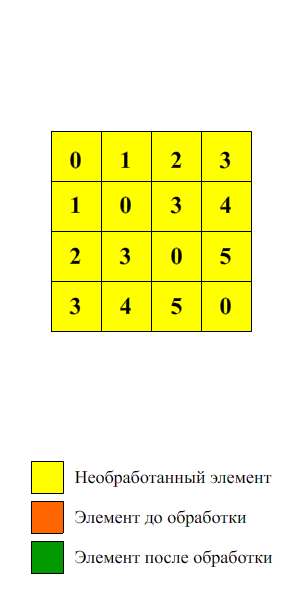
Результаты вычислительных экспериментов

Эксперименты проводились на компьютере с характеристиками:

Процессор - AMD Phenom II X4 945 3 GHz
Оперативная память - 3.25 GB
Операционная система - MS Windows 7 x32
Компилятор - MS Visual Studio 2010

Сначала был реализован последовательный алгоритма Флойда и для него был проведены эксперименты с различным количеством вершин.

Число вершин	Последовательный алгоритм
100	0.038
200	0.317
500	4.618
1000	36.9
2000	292.162

По результатам выполненных экспериментов подтвердилось, что характер зависимости времени работы алгоритма Флойда от количества вершин в графе является кубическим (при увеличении количества данных в два раза время работы алгоритма увеличивается в восемь раз и т.д.).

Затем был реализован параллельный алгоритма Флойда и для него был проведены эксперименты с различным количеством вершин, а так же с различным количеством процессов (2 и 4).

Число вершин	2 процесса	Ускорение	4 процесса	Ускорение
100	0.018066	2.1	0.010033	3.8
200	0.144018	2.2	0.074333	4.2
500	2.24964	2.0	1.132426	4.0
1000	18.023488	2.0	9.466067	3.9
2000	145.475483	2.0	76.889873	3.8

Теоретическое ускорение алгоритма равно числу процессоров p. Ускорение, полученное в результате экспериментов тоже приближенно равно p. Значит, полученные практические результаты обосновали теоретические оценки.

Об авторе

Работу выполнил Горячев Никита, группа 8410.