Последовательный алгоритм в прямом виде достаточно сложен для распараллеливания (сравнение пар значений упорядочиваемого набора данных происходит строго последовательно)поэтому в параллельной версии программы используется не сам этот алгоритм, а его модификация, а именно алгоритм чет-нечетной перестановки:
Алгоритм чет-нечетной перестановки:
В алгоритм сортировки вводятся два разных правила выполнения итераций метода: в зависимости от четности или нечетности номера итерации сортировки для обработки выбираются элементы с четными или нечетными индексами соответственно, сравнение выделяемых значений всегда осуществляется с их правыми соседними элементами. Таким образом, на всех нечетных итерациях сравниваются пары
(a1, a2), (a3, a4), ..., (an-1,an) (при четном n),
а на четных итерациях обрабатываются элементы (a2, a3), (a4, a5), ..., (an-2,an-1).
После n-кратного повторения итераций сортировки исходный набор данных будет упорядоченным.
Определим теперь сложность рассмотренного параллельного алгоритма упорядочивания данных. Как отмечалось ранее, на начальной стадии работы метода каждый процессор проводит упорядочивание своих блоков данных (размер блоков при равномерном распределении данных является равным n/p). Предположим, что данная начальная сортировка может быть выполнена при помощи быстродействующих алгоритмов упорядочивания данных, тогда трудоемкость начальной стадии вычислений можно определить выражением вида:
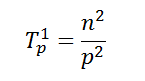
Далее, на каждой выполняемой итерации параллельной сортировки взаимодействующие пары процессоров осуществляют передачу блоков между собой, после чего получаемые на каждом процессоре пары блоков объединяются при помощи процедуры слияния. Общее количество итераций не превышает величины p, и, как результат, общее количество операций этой части параллельных вычислений оказывается равным:
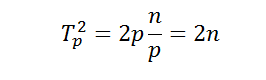
С учетом полученных соотношений показатели эффективности и ускорения параллельного метода сортировки имеют вид:
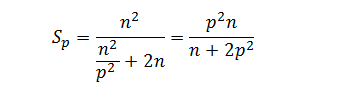
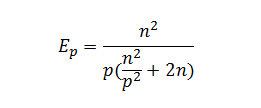
Расширим приведенные выражения – учтем длительность выполняемых вычислительных операций и оценим трудоемкость операции передачи блоков между процессорами. При использовании модели Хокни общее время всех выполняемых в ходе сортировки операций передачи блоков можно оценить при помощи соотношения вида:
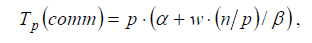
где α – латентность, β – пропускная способность сети передачи данных, а w есть размер элемента упорядочиваемых данных в байтах.
С учетом трудоемкости коммуникационных действий общее время выполнения параллельного алгоритма сортировки определяется следующим выражением:
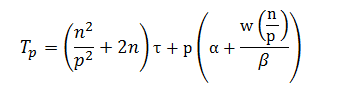
где τ есть время выполнения базовой операции сортировки.
#define SIZE_OF_ARRAY 10000
void sort (int *pMas, int size)
{
for (int i = size - 2; i >= 0; i--)
for (int j = 0; j <= i; j++)
if (pMas[j] > pMas[j + 1])
pMas[j] ^= pMas[j+1] ^= pMas[j] ^= pMas[j+1];
}
void mergeArrays (int *pMas1, int size1, int *pMas2, int size2, int *result)
{
int i = 0, j = 0, k = 0;
while (i < size1 && j < size2)
if (pMas1[i] < pMas2[j])
result[k++] = pMas1[i++];
else
result[k++] = pMas2[j++];
if (i == size1)
while (j < size2)
result[k++] = pMas2[j++];
if(j == size2)
while (i < size1)
result[k++] = pMas1[i++];
}
void initArray (int *pMas, int size)
{
for (int i = 0; i < size; i++)
pMas[i] = rand() % 1000;
}
void outputArray (const char *pFileName, int *pMas, int size)
{
FILE *file = fopen(pFileName, "wt");
for (int i = 0; i < size; i++)
fprintf(file, "%d: %d\n", i, pMas[i]);
fclose(file);
}
int main (int argc, char **argv)
{
double startTime, stopTime;
int *data;
int *resultant_array;
int *sub;
int m;
int r;
int s;
int move;
MPI_Status status;
MPI_Init (&argc, &argv);
int rank, count;
MPI_Comm_rank (MPI_COMM_WORLD, &rank);
MPI_Comm_size (MPI_COMM_WORLD, &count);
if (rank == 0)
{
s = SIZE_OF_ARRAY / count;
r = SIZE_OF_ARRAY % count;
data = new int[SIZE_OF_ARRAY + s - r];
initArray (data, SIZE_OF_ARRAY);
outputArray ("input.txt", data, SIZE_OF_ARRAY);
if (r != 0)
{
for (int i = SIZE_OF_ARRAY; i < SIZE_OF_ARRAY + s - r; i++)
data[i] = 0;
s = s + 1;
}
startTime = MPI_Wtime();
MPI_Bcast (&s, 1, MPI_INT, 0, MPI_COMM_WORLD);
resultant_array = new int[s];
MPI_Scatter (data, s, MPI_INT, resultant_array, s, MPI_INT, 0, MPI_COMM_WORLD);
sort (resultant_array, s);
}
else
{
MPI_Bcast (&s, 1, MPI_INT, 0, MPI_COMM_WORLD);
resultant_array = new int[s];
MPI_Scatter (data, s, MPI_INT, resultant_array, s, MPI_INT, 0, MPI_COMM_WORLD);
sort (resultant_array, s);
}
move = 1;
while (move < count)
{
if (rank % (2 * move) == 0)
{
if (rank + move < count)
{
MPI_Recv (&m, 1, MPI_INT, rank + move, 0, MPI_COMM_WORLD, &status);
sub = new int [m];
MPI_Recv (sub, m, MPI_INT, rank + move, 0, MPI_COMM_WORLD, &status);
int *tmp = new int[s + m];
mergeArrays (resultant_array, s, sub, m, tmp);
resultant_array = tmp;
s = s + m;
}
}
else
{
int near = rank - move;
MPI_Send (&s, 1, MPI_INT, near, 0, MPI_COMM_WORLD);
MPI_Send (resultant_array, s, MPI_INT, near, 0, MPI_COMM_WORLD);
break;
}
move = move * 2;
}
if (rank == 0)
{
stopTime = MPI_Wtime();
double t1 = stopTime- startTime;
printf("Time on %d: %lf\n", count, t1);
startTime = MPI_Wtime();
sort(data,SIZE_OF_ARRAY);
stopTime = MPI_Wtime();
double t2 = stopTime - startTime;
printf("Time on 1: %lf\n", t2);
printf("A: %f\n", t2/t1);
outputArray ("output.txt", resultant_array, SIZE_OF_ARRAY);
}
MPI_Finalize ();
return 0;
}
Работу выполнили студенты группы 8409 Федоров А.В. и Секачев Е.



