Постановка задачи.
Задача о нахождении минимального остовного дерева часто встречается в подобной постановке: допустим, есть n городов, которые необходимо соединить дорогами, так, чтобы можно было добраться из любого города в любой другой (напрямую или через другие города). Разрешается строить дороги между заданными парами городов и известна стоимость строительства каждой такой дороги. Требуется решить, какие именно дороги нужно строить, чтобы минимизировать общую стоимость строительства.
Эта задача может быть сформулирована в терминах теории графов как задача о нахождении минимального остовного дерева в графе, вершины которого представляют города, рёбра — это пары городов, между которыми можно проложить прямую дорогу, а вес ребра равен стоимости строительства соответствующей дороги.
Цель данной работы - реализация алгоритма, вычисляющего минимальное остовное дерево.
Результатом работы программы должно быть получено множество рёбер минимального остовного дерева и замер времени вычисления.
Требуется реализовать последовательный и параллельный алгоритмы. Реализацию параллельного алгоритма провести средствами MPI.
Метод решения ( последовательная версия ).
Алгоритм:
0. Вводится множество T вершин, которые уже добавлены в результирующее дерево.
1. Выбирается произвольная вершина и добавляется в множество T.
2. До тех пор пока в дерево не добавлены все вершины делать:
a. Найти вершину, расстояние от дерева T до которой минимально.
b. Добавить ее к дереву.
Анализ эффективности.
В идеальном случае оценки эффективности для оценки сложности параллельного алгоритма Прима для нахождения минимального охватывающего дерева вычисляются по следующим формулам:
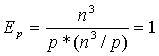
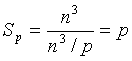
В ходе вычислений в зависимости от количества выбранных вершин вычислительная нагрузка на процессоры может различаться.
Для уточнения полученных показателей эффективности оценим более точно количество выполненных операций и затраты на передачу данных между процессами.
На каждом шаге параллельный алгоритм выбирает вершину с минимальным расстоянием до строящегося дерева и корректирует веса di для каждой вершины. Количество операций при каждой из этих процедур ограничено числом 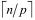 . Поэтому на выполнение n итераций алгоритм затратит следующее время ( r - время на выполнение элементарной операции ):
. Поэтому на выполнение n итераций алгоритм затратит следующее время ( r - время на выполнение элементарной операции ):
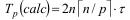
Сборка данных на одном процессоре может быть выполнена за 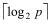 итераций.
итераций.
Следовательно, на передачу данных от всех процессоров системы корневому будет затрачено время:
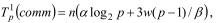
где a - латентность сети передачи данных, B - пропускная способность сети, w - размер одного элемента данных в байтах.
Операция рассылки одного элемента данных требует операций и может быть выполнена за время
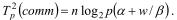
Тогда суммарное время работы алгоритма может быть представлено соотношением:
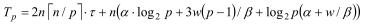
Это выражение показывает, что при больших n время работы параллельного алгоритма будет определяться квадратичной частью выражения и ускорение будет близко к идеальному. При малых же n ускорение будет определятся линейной частью выражения и значение ускорения будет низким.
Демонстрация
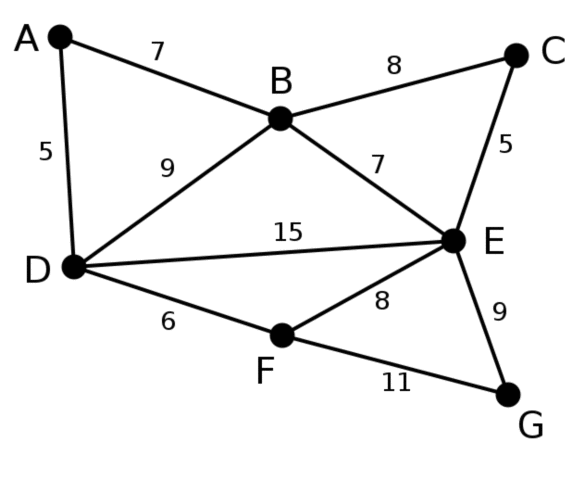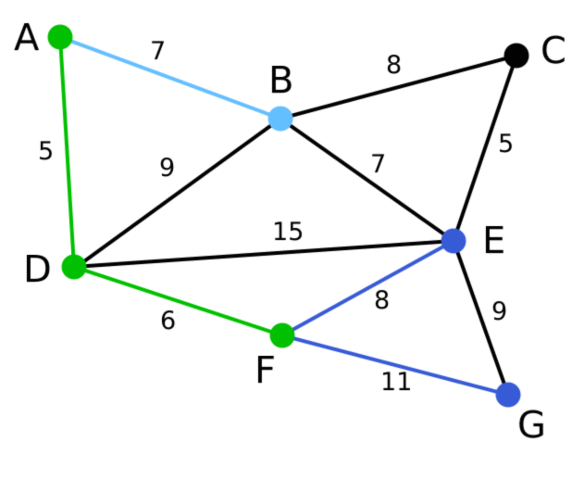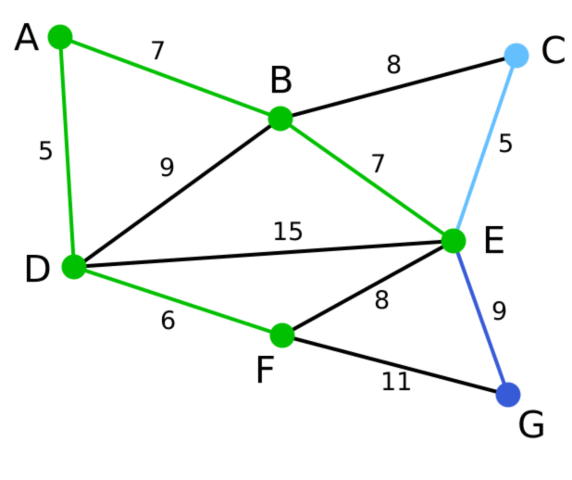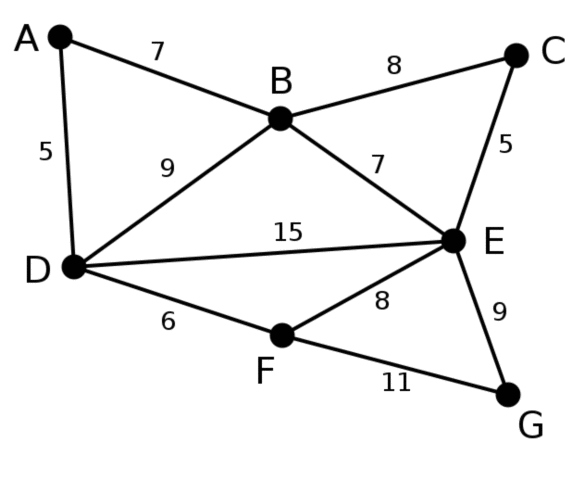
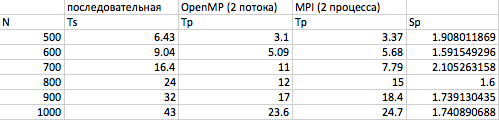
Результаты экспериментов
Об авторах
Лавренов И.П., Медведев М.С.
Группа 84-09



