При большом числе неизвестных метод Гаусса становится весьма сложным в плане вычислительных и временных затрат. Поэтому иногда удобнее использовать приближенные (итерационные) численные методы, метод Якоби относится к таким.
В работе требуется решить систему линейных алгебраических уравнений вида:
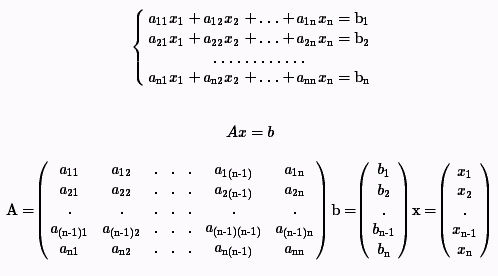
При предположении, что диагональные коэффициенты ненулевые.
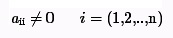
Метод решения
Решив 1-ое уравнение системы относительно x1 получим:
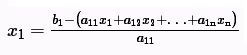
2-ое - относительно x2 , n-ое - относительно xn
В итоге эквивалентная система, в которой диагональные элементы строки выражены через оставщиеся.
Далее вводится некоторое начальное приближение - вектор x(0)=[b1/a11, ... ,bi/aii, ... ,bn/ann], затем используя x(1) находится x(2).
Данный процесс называется итерационным, условием окончания является достижение заданной точности (система сходится и есть решение) или прерывание процесса. Процесс прерывается когда число итераций превышает заданное допустимое количество, при этом система не сходится либо заданное количество итераций не хватило для достижения требуемой точности.
Итерационный процесс. Верхний индекс в скобках - номер итерации.
Если последовательность приближений (x(0),x(1),...,x(k+1),...) имеет предел
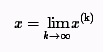
то этот предел является решением.
k=1,2,3,...N-1. , N-1 - заданное количество итераций
Достаточный признак сходимости метода Якоби:
Если в системе выполняется диагональное преобладание, то метод Якоби сходится.
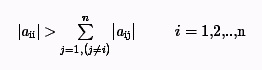
Критерий окончания итераций при достижении требуемой точности имеет вид:
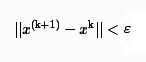
где ε - заданная точность вычисления
Параллельная схема
При распараллеливании алгоритма предполагается, что размерность системы больше числа процессоров. Каждый процессор считает “свои” элементы вектора Х=(x1,x2,x3,...,xn).
Перед началом выполнения метода на каждый процессор рассылаются необходимые данные:
1) размерность системы N
2) начальное приближение X0
3) строки матрицы A
4) элементы вектора свободных членов b.
После получения необходимой информации каждый процессор будет вычислять соответствующие компоненты вектора X и передавать их главному процессору. Главный процессор при получении очередного приближения решения Xk должен сравнить его с предыдущим приближением Xk-1. Если норма разности этих векторов:
||Xk – Xk-1|| = max {|Xk,i – Xk,i-1|, i = 1,1,…n}
окажется меньше или равной заданной точности (ε), то вычисления закончатся. В противном случае вектор Xk поэлементно будет разослан всем процессам и будет вычисляться очередное приближение решения.
Анализ эффективности
Время, затраченное на последовательное выполнение алгоритма, выражается следующей формулой: T = k * (2*n^2 - n), где k – число выполненных итераций, а n – число уравнений.
Время, затраченное на параллельное выполнение алгоритма на p процессорах без учета затрат на передачу данных, выражается формулой: T(p) = k/p * (2*n^2 - n)
Тогда ускорение равно: S = T(1) / T(p) = p
Эффективность: E = T1 / p*Tp = 1
Разработанный способ параллельных вычислений позволяет достичь идеальных показателей ускорения и эффективности.
Определим время, затрачиваемое на передачу данных. Для этого используем модель Хокни.
Первоначальная рассылка данных требует следующее время: Tcomm1 = (p-1) * (4*alfa + (n^2 / p + n) / betta), где alfa - латентность, betta - пропускная способность сети
Передача данных, выполняемая в итерационном процессе, затрачивает следующее время: Tcomm2 = k * (p-1) * (3*alfa + (n / p + n) / betta), где k - количество выполненных итераций
В итоге общее время передачи данных выражается формулой: Tcomm = (p-1) * (4*alfa + (n^2 / p + n) / betta) + k * (p-1) * (3*alfa + (n / p + n) / betta)
Это время зависит от числа итераций. Как правило, их количество меньше числа уравнений n. Значит время на передачу данных можно оценить величиной: Tcomm = O(n^2)
В свою очередь и ко времени выполнения алгоритма применима та же оценка: T = O(n^2)
Если число итераций будет сравнимо с n, то для времени выполнения алгоритма будет справедлива уже другая оценка: T = O(n^3)
Демонстрация
На каждой итерации итерации вычисление (k+1)-ого вектора происходит по следующей схеме:
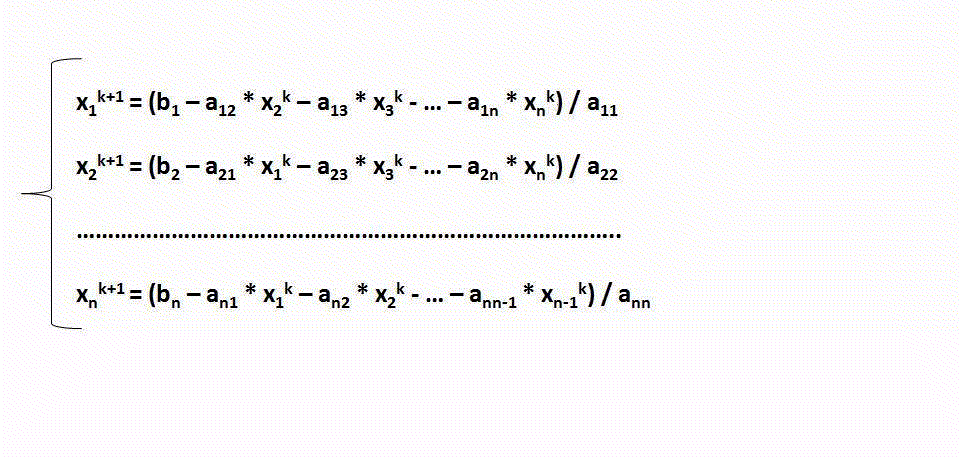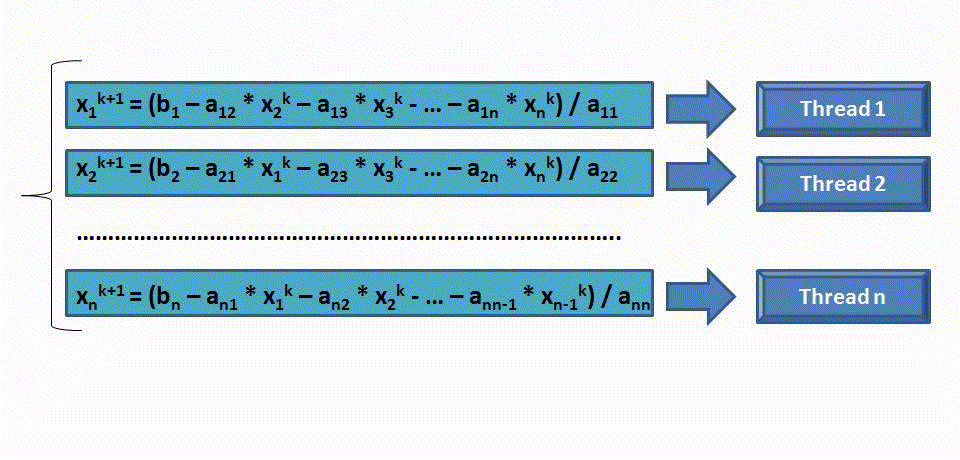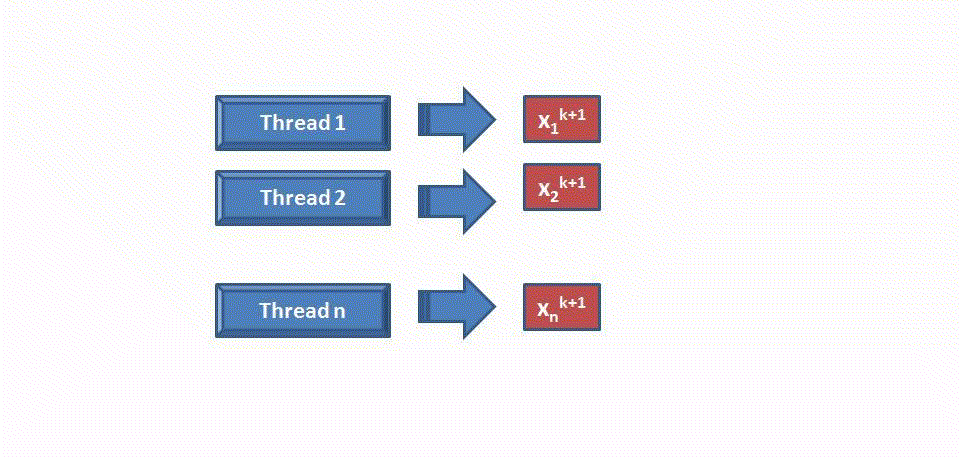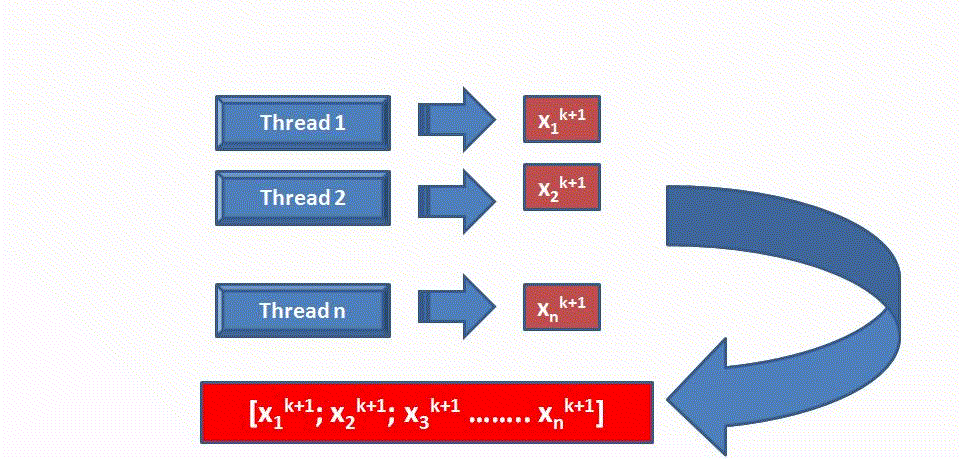
Результаты вычислительных экспериментов
Эксперименты проводились на следующем компьютере:
Процессор Intel(R) Core(TM) i7-2630QM CPU @ 2.00GHz, ОС Windows 8 64-bit.
Результаты программы(MPI)
Размер матрицы
Последовательный алгоритм (1 процесс)
4 процесса
2 процесса
Параллельный алгоритм (мс)
Теор. время паралл. алгоритма (мс)
Ускорение
Параллельный алгоритм (мс)
Теор. время паралл. алгоритма (мс)
Ускорение
3000*3000
33
15
8,25
2,2
18
16,5
1,8
6000*6000
136
59
34
2,3
72
68
1,8
9000*9000
314
132
78,5
2,37
163
157
1,9
Результаты программы(OpenMP)
Эксперименты проводились на следующих компьютерах:
1) Процессор Intel(R) Core(TM) i7-2630QM CPU @ 2.00GHz, ОС Windows 8 64-bit.
2) Процессор AMD Phenom(tm) II X4 945, ОС Windows 7 64-bit.
3) Процессор AMD Turion(tm) II P540 Dual-Core Processor 2.40GHz, ОС Windows 7 64-bit.
Каждое значение, представленное в данной таблице, является средним временем на основе 25 экспериментов.
