Постановка задачи

С развитием систем сообщения в жизни человека естественным образом появились транспортные задачи, т.е. задачи поиска оптимальных путей. Любая транспортная задача хорошо моделируется взвешенным графом. Вершинами графа моделируются узлы системы, рёбрами — линни связи. Веса рёбер графа определяют расходы на использование соответствующих линий. Существует целый класс алгоритмов поиска оптимальных путей, но в данной работе разобран только алгоритм Флойда и произведена его последовательная и параллаельная реализация. Этот алгоритм был разработан Робертом Флойдом и Стивеном Уоршеллом в 1962 году.

Метод решения

Этот алгоритм более общий по сравнению с алгоритмом Дейкстры, так как он находит кратчайшие пути между любыми двумя узлами сети. В этом алгоритме сеть представлена в виде квадратной матрицы с n строками и n столбцами. Элемент (i, j) равен расстоянию d_ij от узла i к узлу j, которое имеет конечное значение, если существует дуга (i, j), и равен бесконечности в противном случае.     Покажем сначала основную идею метода Флойда. Пусть есть три узла i, j и k> и заданы расстояния между ними (рис. 1). Если выполняется неравенство d_ij + d_jk < d_ik, то целесообразно заменить путь i -> k путем i -> j -> k. Такая замена (которая обычно называется) выполняется систематически в процессе выполнения алгоритма Флойда.

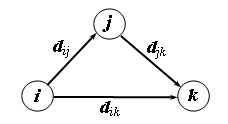
Рис.1. Треугольный оператор

Исходной информацией для задачи поиска кратчайших путей является взвешенный граф G = (V, R), содержащий n вершин (|V|= n), в котором каждому ребру графа приписан неотрицательный вес. Граф будем полагать ориентированным, т.е., если из вершины i есть ребро в вершину j, то из этого не следует наличие ребра из j в i. В случае, если вершины все же соединены взаимообратными ребрами, то веса, приписанные им, могут не совпадать. Для поиска минимальных расстояний между всеми парами пунктов назначения Флойд предложил алгоритм, сложность которого имеет порядок n^3 . В общем виде данный алгоритм может быть представлен следующим образом:

// Serial Floyd algorithm

for (k = 0; k < n; k++)

for (i = 0; i < n; i++) {

for (j = 0; j < n; j++)

A[i,j] = min(A[i,j],A[i,k]+A[k,j]);

}

Как можно заметить, в ходе выполнения алгоритма матрица смежности A изменяется, после завершения вычислений в матрице A будет храниться требуемый результат - длины минимальных путей для каждой пары вершин исходного графа.

Параллельная схема

Как следует из общей схемы алгоритма Флойда, основная вычислительная нагрузка при решении задачи поиска кратчайших путей состоит в выполнении операции выбора минимального значения. Данная операция является достаточно простой и ее распараллеливание не приведет к заметному ускорению вычислений. Более эффективный способ организации параллельных вычислений может состоять в одновременном выполнении нескольких операций обновления значений матрицы A.

Покажем корректность такого способа организации параллелизма. Для этого нужно доказать, что операции обновления значений матрицы A на одной и той же итерации внешнего цикла k могут выполняться независимо. Иными словами, следует показать, что на итерации k не происходит изменения элементов A[i,k] и A[k,j] ни для одной пары индексов (i, j). Рассмотрим выражение, по которому происходит изменение элементов матрицы A:

A[i,j] = min (A[i,j], A[i,k] + A[k,j]).

Для i=k получим

A[k,j] = min (A[k,j], A[k,k] + A[k,j]),

но тогда значение A[k,j] не изменится, т.к. A[k,k]=0.

Для j=k выражение преобразуется к виду

A[i,k] = min (A[i,k], A[i,k] + A[k,k]),

что также показывает неизменность значений A[i,k]. Как результат, необходимые условия для организации параллельных вычислений обеспечены, и, тем самым, в качестве базовой подзадачи может быть использована операция обновления элементов матрицы A (для указания подзадач будем применять индексы обновляемых в подзадачах элементов).

Выполнение вычислений в подзадачах становится возможным только тогда, когда каждая подзадача (i, j) содержит необходимые для расчетов элементы A[i,j], A[i,k], A[k,j] матрицы A. Для исключения дублирования данных разместим в подзадаче (i, j) единственный элемент A[i,j], тогда получение всех остальных необходимых значений может быть обеспечено только при помощи передачи данных.

В работе использовалось горизонтальное разбиение матрицы, т.е. каждому процессу передавалось несколько строк матрицы, с которыми он выполнял необходимые действия.

Параллельный алгоритм Флойда заключается в том, что на k-й итерации мы отсылаем k-ю строку всем процессам, а затем каждый процесс выполняет последовательный алгоритм Флойда для своей полосы матрицы смежности, одновременно обновляя значение матрицы.

Анализ эффективности

Как было указано выше, общая трудоёмкость последовательного алгоритма Флойда O(n^3).

Для параллельного алгоритма на отдельной итерации каждый процессор выполняет обновление элементов матрицы A. Всего в подзадачах n^2/p таких элементов, число итераций алгоритма равно n, таким образом, показатели ускорения и эффективности параллельного алгоритма Флойда имеют вид (p – число процессоров):

Sp = n^3/(n^3/p) = p,

Ep = n^3/(p(n^3⁄p)) = 1.

Общий анализ сложности дает идеальные показатели эффективности параллельных вычислений.

Для параллельного выполнения алгоритма Флойда над графом, содержащим n вершин, требуется выполнение n итераций алгоритма, на каждой из которых параллельно выполняется обновление всех элементов матрицы смежности. Значит, время выполнения вычислений составляет:

Tp = n^2(n/p)τ,

где τ есть время выполнения операции выбора минимального значения, однако при этом не учтены коммуникационные операции.

Коммуникационная операция, выполняемая на каждой итерации алгоритма Флойда, состоит в передаче одной из строк матрицы A всем процессорам вычислительной системы. Выполнение такой операции может быть выполнено за log2 p шагов.

Общая длительность выполнения коммуникационных операций:

Tp(comm) = n log2 p (α + wn/β),

где α – латентность сети передачи данных, β – пропускная способность сети, w – размер элемента матрицы в байтах.

Общее время выполнения параллельного алгоритма Флойда:

Tp(общ) = n^3/p τ + n log2 p (α + wn/β).

Результаты вычислительных экспериментов

Тесты проводились на четырехъядерном процессоре intel core i5 2500k. Использовалось только три процесса и потока, что позволяет минимизировать воздействие сторонних приложений на время работы алгоритма. Время указано в мс.

OpenMp

MPI

Об авторах

Работу выполнили студенты группы 8409 Чистяков Александр и Люльков Александр.