Постановка задачи

Нахождение кратчайшего пути на сегодняшний день является жизненно необходимой задачей и используется практически везде, начиная от нахождения оптимального маршрута между двумя объектами на местности (например, кратчайший путь от дома до университета), в системах автопилота, для нахождения оптимального маршрута при перевозках, коммутации информационного пакета в сетях и т.п.

Основная цель работы заключается в том, чтобы для взвешенного, ориентированного графа G=(V,R) найти кратчайшие пути для каждой его пары вершин.

Метод решения

Данная задача решается с использованием алгоритма Флойда.

Этот метод непосредственно основывается на том факте, что в графе с положительными весами ребер всякий неэлементарный (содержащий более 1 ребра) кратчайший путь состоит из других кратчайших путей.

В алгоритме Флойда используется матрица A размером nxn, в которой вычисляются длины кратчайших путей. Элемент A[i,j] равен расстоянию от вершины i к вершине j, которое имеет конечное значение, если существует ребро (i,j), и равен бесконечности в противном случае.

Основная идея алгоритма. Пусть есть три вершины i,j,k и заданы расстояния между ними. Если выполняется неравенство:

A[i,k]+A[k,j] < A[i,j],

то целесообразно заменить путь i->j путем i->k->j. Такая замена выполняется систематически в процессе выполнения данного алгоритма.

Шаг 0. Определяем начальную матрицу расстояния A₀ и матрицу последовательности вершин S₀. Каждый диагональный элемент обеих матриц равен 0, таким образом, показывая, что эти элементы в вычислениях не участвуют. Полагаем k = 1.

Основной шаг k. Задаем строку k и столбец k как ведущую строку и ведущий столбец. Рассматриваем возможность применения замены описанной выше, ко всем элементам A[i,j] матрицы A_(k-1). Если выполняется неравенство A[i,k]+A[k,j]

1. создаем матрицу A_k путем замены в матрице A_(k-1) элемента A[i,j] на сумму A[i,k]+A[k,j];

2. создаем матрицу S_k путем замены в матрице S_(k-1)элемента S[i,j] на k. Полагаем k = k + 1 и повторяем шаг k.

Таким образом, алгоритм Флойда делает n итераций, после i-й итерации матрица А будет содержать длины кратчайших путей между любыми двумя парами вершин при условии, что эти пути проходят через вершины от первой до i-й. На каждой итерации перебираются все пары вершин, и путь между ними сокращается при помощи i-й вершины.

На псевдокоде алгоритм Флойда может быть представлен следующим образом:

for (k = 0; k < n; k++)

 for (i = 0; i < n; i++)

  for (j = 0; j < n; j++)

   A[i,j] = min(A[i,j], A[i,k]+A[k,j]);

Параллельная схема

Исходя общий вид алгоритма, можно сказать, что он может быть распараллелен в нескольких местах:

1. при выборе минимума;

2. при обновлении матрицы А.

Учитывая простоту операции выбора минимума, можно заключить, что её распараллеливание не приведет к заметному ускорению вычислений. Большее ускорение можно получить при распараллеливании операции обновления матрицы A, другими словами, при обновлении значений матрицы A одновременно в нескольких ячейках.

Как результат, необходимые условия для организации параллельных вычислений обеспечены и, тем самым, в качестве базовой подзадачи может быть использована операция обновления элементов матрицы A (для указания подзадач будем использовать индексы обновляемых в подзадачах элементов). Выполнение вычислений в подзадачах становится возможным только тогда, когда каждая подзадача (i,j) содержит необходимые для расчетов элементы A_ij, A_ik, A_kj матрицы A. Для исключения дублирования данных разместим в подзадаче (i,j) единственный элемент A_ij, тогда получение всех остальных необходимых значений может быть обеспечено только при помощи передачи данных. Таким образом, каждый элемент A_kj строки k матрицы A должен быть передан всем подзадачам (k,j),1 < j < n, а каждый элемент A_ik столбца k матрицы A должен быть передан всем подзадачам (i,k), 1 < i < n.

Массивы в С++ хранятся в памяти построчно. Тогда для ещё большей эффективности распараллеливания алгоритма будем разбивать матрицу A по строкам. Это позволит нам быстро обращаться к соседним ячейкам матрицы, расположенным в одной строчке, «не прыгая по памяти». Учитывая такое разбиение, на каждой итерации распараллеленного алгоритма Флойда подзадаче нужно будет передавать элементы только одной из строк матрицы A.

Анализ эффективности

Общая трудоемкость последовательного алгоритма равна O(n³), поскольку в нём присутствуют вложенные друг в друга три цикла. Для параллельного алгоритма на отдельной итерации каждый процессор выполняет обновление элементов матрицы A. Всего в подзадачах n² таких элементов, учитывая число процессоров p, сложность подзадачи — O(n²⁄p). Число итераций алгоритма равно n. Сложность всего алгоритма — O(n³⁄p). Таким образом, показатели ускорения и эффективности параллельного алгоритма Флойда имеют вид:

S_p(n)=(T₁(n))/(T_p(n))=n³/((n³⁄p))=p,

E_p(n)=(T₁(n))/(p⋅T_p(n))=(S_p(n))/p=1.

Таким образом, общий анализ сложности дает идеальные показатели эффективности параллельных вычислений. Для уточнения полученных соотношений введем в полученное выражения время выполнения базовой операции выбора минимального значения и учтём затраты на выполнение операций передачи данных между процессами.

Коммуникационная операция, выполняемая на каждой итерации алгоритма Флойда, состоит в передаче одной из строк матрицы A всем процессорам вычислительной системы. Выполнение такой операции может быть выполнено за log₂⁡p шагов. С учетом количества итераций алгоритма Флойда, длительность выполнения коммуникационных операций может быть определена как:

T_p=n⋅log₂⁡p⋅(α+ωn⁄β),

где α – латентность сети передачи данных, β – пропускная способность сети, ω – размер элемента матрицы в байтах.

С учетом полученных соотношений общее время выполнения параллельного алгоритма Флойда составляет:

T_p=n²(n⁄p)τ+n⋅log₂⁡p⋅(α+ωn⁄β),

где τ есть время выполнения операции выбора минимального значения.

Демонстрация

Представлена работа параллельного алгоритма Флойда над матрицей смежности графа.

Результаты вычислительных экспериментов

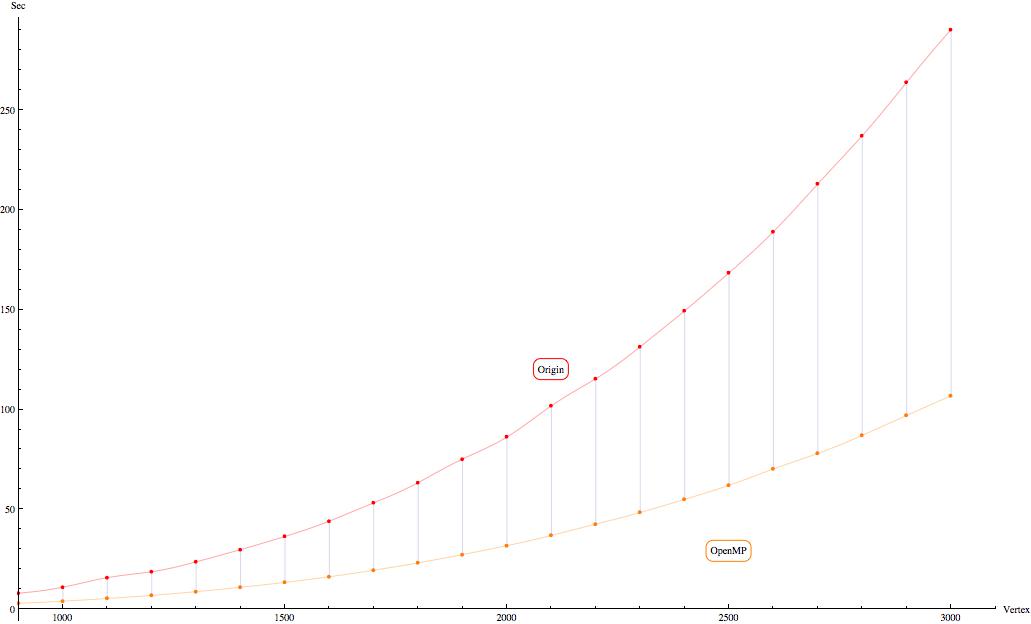
Сравнение обычной версии (график Origin) и распараллеленной с помощью OpenMP (график OpenMP)

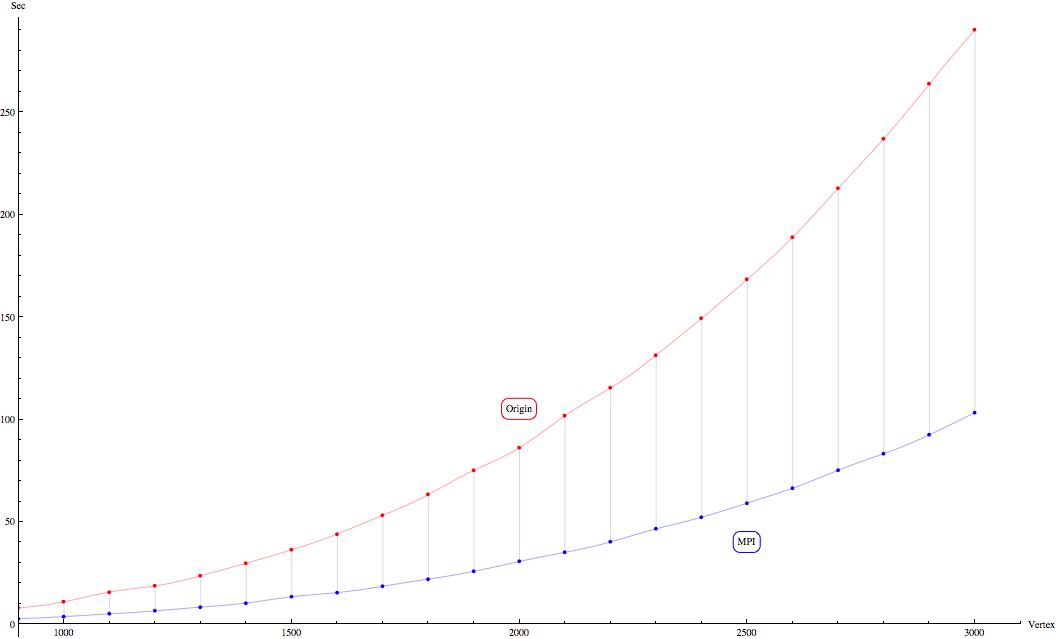
Сравнение обычной версии (график Origin) и распараллеленной с помощью MPI (график MPI)

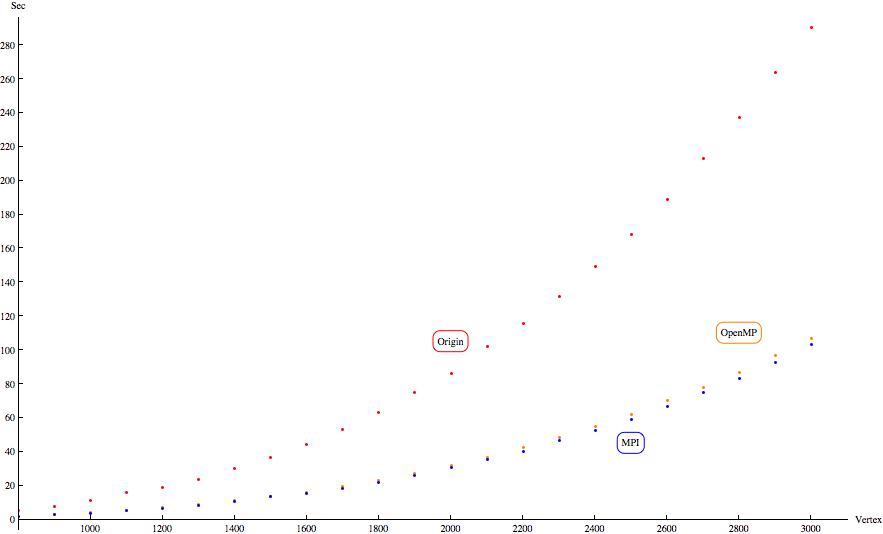
Общий график производительности для всех версий (в осях "Число вершин" - "Секунды")