Постановка задачи

Пусть даны две прямоугольные матрицы A и B размерности m*n и p*q соответственно.

Тогда, если число столбцов матрицы A равно числу строк матрицы B, то есть n=p, то определена матрица C размерностью m*q называемая их произведением:

где:

 

Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором.

Постановка задачи

1) Реализовать последовательный алгоритм перемножения матриц.

2) Реализовать программу блочного умножения матриц (Алгоритм Фокса), используя технологии MPI и OpenMP.

3) Рассчитать теоретическое ускорение и эффективность.

4) Провести набор тестов. Сравнить ускорение последовательного и параллельных (с использованием MPI и OpenMP) алгоритмов.

Описание алгоритма

Используется блочная схема разбиения матриц. При таком способе разделения данных исходные матрицы А, В и результирующая матрица С представляются в виде наборов блоков. Далее предполагается что все матрицы являются квадратными размера n×n, количество блоков по горизонтали и вертикали одинаково и равно q (т.е. размер всех блоков равен k×k, k=n/q). При таком представлении данных операция матричного умножения матриц А и B в блочном виде может быть представлена так:



За основу параллельных вычислений для матричного умножения при блочном разделении данных принят подход, при котором базовые подзадачи отвечают за вычисления отдельных блоков матрицы C и при этом в подзадачах на каждой итерации расчетов располагается только по одному блоку исходных матриц A и B. Для нумерации подзадач будем использовать индексы размещаемых в подзадачах блоков матрицы C, т.е. подзадача (i,j) отвечает за вычисление блока C_ij – тем самым, набор подзадач образует квадратную решетку, соответствующую структуре блочного представления матрицы C.

В соответствии с алгоритмом Фокса в ходе вычислений на каждой базовой подзадаче (i,j) располагается четыре матричных блока:

1. Блок C_ij матрицы C, вычисляемый подзадачей;
2. Блок A_ij матрицы A, размещаемый в подзадаче перед началом вычислений;
3. Блоки A'_ij , B'_ij матриц A и B, получаемые подзадачей в ходе выполнения вычислений.

Выполнение параллельного метода включает:

1. Этап инициализации, на котором каждой подзадаче (i,j) передаются блоки A_ij, B_ij и обнуляются блоки C_ij на всех подзадачах;
2. Этап вычислений, в рамках которого на каждой итерации l, l от нуля (включительно) до q, осуществляются следующие операции:
   a. Для каждой строки i (i от нуля включительно и строго до q) блок A_ij подзадачи (i,j) пересылается на все подзадачи той же строки i решетки; индекс j, определяющий положение подзадачи в строке, вычисляется в соответствии с выражением j=(i+l)mod q, где mod есть операция получения остатка от целочисленного деления;
   b. Полученные в результаты пересылок блоки A'_ij, B'_ij каждой подзадачи (i,j) перемножаются и прибавляются к блоку C_ij
   c. Блоки B'_ij каждой подзадачи (i,j) пересылаются подзадачам, являющимся соседями сверху в столбцах решетки подзадач (блоки подзадач из первой строки решетки пересылаются подзадачам последней строки решетки).

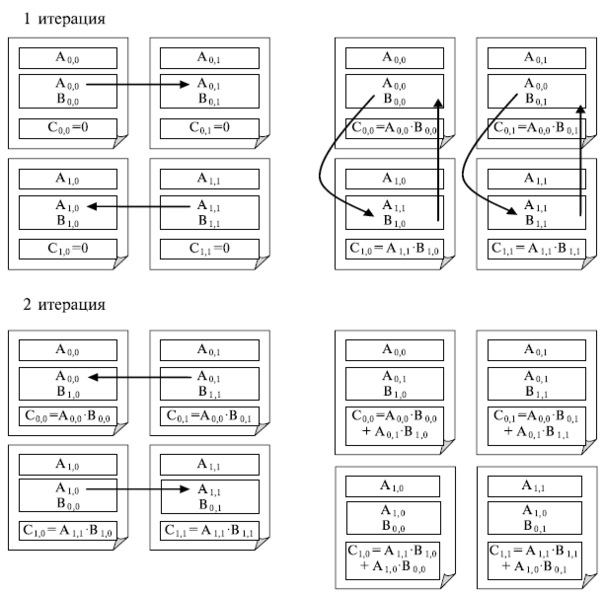
Масштабирование и распределение подзадач по процессорам

В рассмотренной схеме параллельных вычислений количество блоков может варьироваться в зависимости от выбора размера блоков – эти размеры могут быть подобраны таким образом, чтобы общее количество базовых подзадач совпадало с числом процессоров p. Так, например, в наиболее простом случае, когда число процессоров представимо в виде p=s^2 (т.е. p является полным квадратом), можно выбрать количество блоков в матрицах по вертикали и горизонтали равным s(т.е. q=s). Такой способ определения количества блоков приводит к тому, что объем вычислений в каждой подзадаче является одинаковым и тем самым достигается полная балансировка вычислительной нагрузки между процессорами.
Для эффективного выполнения алгоритма Фокса, в котором базовые подзадачи представлены в виде квадратной решетки и в ходе вычислений выполняются операции передачи блоков по строкам и столбцам решетки подзадач, наиболее адекватным решением является организация множества имеющихся процессоров также в виде квадратной решетки. В этом случае можно осуществить непосредственное отображение набора подзадач на множество процессоров – базовую подзадачу (i,j) следует располагать на процессоре P_ij. Необходимая структура сети передачи данных может быть обеспечена на физическом уровне, если топология вычислительной системы имеет вид решетки или полного графа.

Реализация алгоритма

Реализация с использованием MPI.

Основные этапы разработки параллельного алгоритма:

1. Создание виртуальной декартовой топологии

2. Определение размеров объектов и ввод исходных данных

3. Завершение процесса вычислений

4. Распределение данных между процессами

5. Начало реализации параллельного алгоритма матричного умножения

6. Рассылка блоков матрицы А

7. Циклический сдвиг блоков матрицы В вдоль столбцов процессорной решетки

8. Умножение матричных блоков

9. Сбор результатов

1. Создание виртуальной декартовой топологии

В функции main объявим основные переменные:
ProcNum – количество процессов;
ProcRank – ранг процесса;
pAMatrix – матрица А;
pBMatrix – матрица В;
pCMatrix – матрица С;
Size – размер матриц.

Для эффективного выполнения алгоритма Фокса необходимо организовать доступные процессы MPI-программы в виртуальную топологию в виде двумерной квадратной решетки. Это возможно только в случае, когда число доступных процессов является полным квадратом (ProcNum=GridSize×GridSize).
Функция CreateGridCommunicators создает коммуникатор в виде двумерной квадратной решетки, определяет координаты каждого процесса в этой решетке, а также создает коммуникаторы отдельно для каждой строки и каждого столбца.
Создание решетки производится при помощи функции MPI_Cart_create (вектор Periodic определяет возможность передачи сообщений между граничными процессами строк и столбцов создаваемой решетки). После создания решетки каждый процесс параллельной программы будет иметь координаты своего положения в решетке; получение этих координат обеспечивается при помощи функции MPI_Cart_coords.
Формирование топологий завершается созданием множества коммуникаторов для каждой строки и каждого столбца решетки в отдельности (функция MPI_Cart_sub ).

2. Определение размеров объектов и ввод исходных данных

С помощью функции ProcessInitialization определяем параметры решаемой задачи (размеры матриц и их блоков), выделяем память для хранения данных и формируем исходные данные при помощи датчика случайных чисел. Всего в каждом процессе должна быть выделена память для хранения четырех блоков – для указателей на выделенную память используются переменные pAblock, pBblock, pCblock, pMatrixAblock. Первые три указателя определяют блоки матриц A, B и C соответственно. Следует отметить, что содержимое блоков pAblock и pBblock постоянно меняется в соответствии с пересылкой данных между процессами, в то время как блок pMatrixAblock матрицы A остается неизменным и применяется при рассылках блоков по строкам решетки процессов.
Для определения элементов исходных матриц будем использовать функцию RandomDataInitialization.

3. Завершение процесса вычислений

Функция ProcessTermination обеспечивает корректное завершение работы приложения и освобождение памяти, выделенной динамически в ходе выполнения приложения.

4. Распределение данных между процессами

Исходные матрицы расположены на ведущем процессе, который расположен в левом верхнем углу процессорной решетки. Нужно распределить матрицы поблочно между процессами так, чтобы блоки Aij и Bij были помещены на процессе, расположенном на пересечении i-ой строки и j-ого столбца процессорной решетки.
Функция CheckerboardMatrixScatter распределяет матрицу поблочно между процессами решетки процессов.
Функция DataDistribution распределяет исходные матрицы А и В поблочно между процессами решетки процессов.

5. Начало реализации параллельного алгоритма матричного умножения

Для непосредственного выполнения параллельного алгоритма Фокса умножения матриц предназначена функция ParallelResultCalculation, которая реализует логику работы алгоритма: рассылку блоков матрицы A вдоль строки решетки процессов, выполнение умножения блоков, сдвиг блоков матрицы В вдоль столбца решетки процессов.

6. Рассылка блоков матрицы А

Функция ABlockCommunication для рассылки блоков матрицы А определяет номер рассылающего процесса по формуле: Pivot = (i+iter) mod GridSize, где i – номер строки, копирует содержимое блока pMatrixAblock в буфер pAblock, рассылает блок pAblock при помощи функции MPI_Bcast.

7. Циклический сдвиг блоков матрицы В вдоль столбцов процессорной решетки

Функция BblockCommunication выполняет циклический сдвиг блоков матрицы B по столбцам процессорной решетки. Каждый процесс передает свой блок следующему процессу NextProc в столбце процессов и получает блок, переданный из предыдущего процесса PrevProc в столбце решетки. Выполнение операций передачи данных осуществляется при помощи функции MPI_SendRecv_replace, которая обеспечивает все необходимые пересылки блоков, используя при этом один и тот же буфер памяти pBblock. Кроме того, эта функция гарантирует отсутствие возможных тупиков, когда операции передачи данных начинают одновременно выполняться несколькими процессами при кольцевой топологии сети.

8. Умножение матричных блоков

Функция BlockMultiplication обеспечивает перемножение блоков матриц A и B.

9. Сбор результатов

Процедура сбора результатов повторяет процедуру распределения исходных данных, но этапы необходимо выполнять в обратном порядке: осуществить сбор полосы результирующей матрицы из блоков, расположенных на процессорах одной строки процессорной решетки, собрать матрицу из полос, расположенных на процессорах, составляющих крайний левый столбец процессорной решетки.
Сбор осуществляется при помощи функции MPI_Gather.

Реализация с использованием OpenMP.

Алгоритм Фокса изначально ориентирован на вычислительные системы с распределённой памятью. Предлагаемый им способ распределения блоков между задачами позволяет максимально распараллелить умножение матриц и исключает обращение разными процессами к одним и тем же частям матрицы. В условиях smp системы нет необходимости в передаче данных от одного вычислителя к другому, поэтому классический алгоритм Фокса можно существенно упростить. Теперь нет необходимости выбирать в качестве начального блока один из диагональных блоков матрицы. Достаточно каждому из потоков выделить свою строку блоков матицы А. Таким образом, все потоки имеют доступ на чтение к обеим матрицам, а на запись к разным строкам результирующей матрицы С, и не вызывают конфликтов.

Оценка эффективности

Определим вычислительную сложность данного алгоритма Фокса. Построение оценок будет происходить при условии выполнения всех ранее выдвинутых предположений: все матрицы являются квадратными размера nxn, количество блоков по горизонтали и вертикали являются одинаковым и равным q (т.е. размер всех блоков равен kxk, k=n/q ), процессоры образуют квадратную решетку и их количество равно p=q2.
Как уже отмечалось, алгоритм Фокса требует для своего выполнения q итераций, в ходе которых каждый процессор перемножает свои текущие блоки матриц А и В и прибавляет результаты умножения к текущему значению блока матрицы C.
Примем за Ts - время работы последовательного алгоритма, за Tp - время работы параллельного алгоритма, за S - ускорение, за E - эффективность, за p – количество процессоров.
При применении последовательного алгоритма перемножения матриц число шагов имеет порядок O(n3). С учетом выдвинутых предположений общее количество выполняемых при этом операций будет иметь порядок n3/p. Как результат, показатели ускорения и эффективности алгоритма имеют вид:

Общий анализ сложности снова дает идеальные показатели эффективности параллельных вычислений. Уточним полученные соотношения — для этого укажем более точно количество вычислительных операций алгоритма и учтем затраты на выполнение операций передачи данных между процессорами.
Определим количество вычислительных операций. Сложность выполнения скалярного умножения строки блока матрицы A на столбец блока матрицы В можно оценить как 2(n/q)-1. Количество строк и столбцов в блоках равно n/q и, как результат, трудоемкость операции блочного умножения оказывается равной (n2/p)(2n/q-1). Для сложения блоков требуется n2/p операций. С учетом всех перечисленных выражений время выполнения вычислительных операций алгоритма Фокса может быть оценено следующим образом:


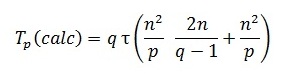
(напомним, что t есть время выполнения одной элементарной скалярной операции).

Оценим затраты на выполнение операций передачи данных между процессорами. На каждой итерации алгоритма перед умножением блоков один из процессоров строки процессорной решетки рассылает свой блок матрицы A остальным процессорам своей строки. Как уже отмечалось ранее, при топологии сети в виде гиперкуба или полного графа выполнение этой операции может быть обеспечено за log2q шагов, а объем передаваемых блоков равен n2/p. Как результат, время выполнения операции передачи блоков матрицы A при использовании модели Хокни может оцениваться как:


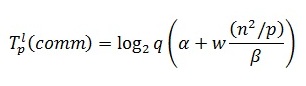
где a – латентность, b – пропускная способность сети передачи данных, а w есть размер элемента матрицы в байтах.

В случае же когда топология строк процессорной решетки представляет собой кольцо, выражение для оценки времени передачи блоков матрицы A принимает вид:



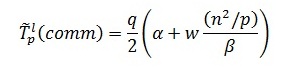
Далее после умножения матричных блоков процессоры передают свои блоки матрицы В предыдущим процессорам по столбцам процессорной решетки (первые процессоры столбцов передают свои данные последним процессорам в столбцах решетки). Эти операции могут быть выполнены процессорами параллельно, и, тем самым, длительность такой коммуникационной операции составляет:



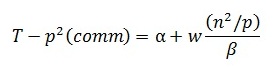
Просуммировав все полученные выражения, можно получить, что общее время выполнения алгоритма Фокса может быть определено при помощи следующих соотношений:


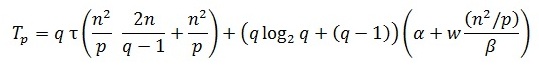
напомним, что параметр q определяет размер процессорной решетки и q = sqrt (p).

Результаты вычислительных экспериментов

Об авторах

Студентки факультета ВМК гр. 83-03: Шульгина Яна, Маматулина Александра