Постановка задачи

Перед нами часто возникает вопрос о размещении некоторого количества элементов в указанном (возрастающем или убывающем) порядке. Это необходимо для улучшения работы с большим количеством данных:
- для решения задачи группировки, когда нужно собрать вместе все элементы с одинаковым значением некоторого признака;
- для последовательного доступа к большим файлам
- при поиске элементов
- для удобства восприятия числовых данных
- и т.д.
От порядка, в котором хранятся элементы в памяти ЭВМ, во многом зависит скорость и простота алгоритмов, предназначенных для их обработки. Таким образом, сортировка является инструментом, полезным в самых различных ситуациях.
Задача сортировки формулируется следующим образом:
Необходимо упорядочить массив a[1..n] по неубыванию (невозрастанию) в соответствии с линейным порядком, заданным на элементах данного массива, путем перестановки его элементов.
Существует много различных методов сортировки, различающихся по эффективности; возможные способы решения этой задачи широко обсуждаются в литературе. В данной работе рассматривается метод сортировки слиянием.

Метод решения

Алгоритм сортировки слиянием был предложен Джоном фон Нейманом в 1945 году и является одним из самых простых алгоритмов сортировки среди «быстрых» алгоритмов. Особенностью этого алгоритма является то, что он работает с элементами массива преимущественно последовательно, благодаря чему именно этот алгоритм используется при сортировке в системах с различными аппаратными ограничениями. Кроме того, сортировка слиянием — чуть ли не единственный алгоритм, который может быть эффективно использован для сортировки таких структур данных, как связанные списки. Последовательная работа с элементами массива значительно увеличивает скорость сортировки в системах с кэшированием.
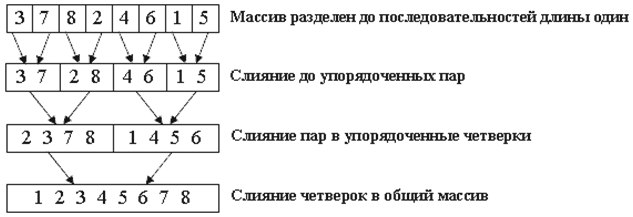
Алгоритм использует принцип «разделяй и властвуй»: задача разбивается на подзадачи меньшего размера, которые решаются по отдельности, после чего их решения комбинируются для получения решения исходной задачи. Алгоритм сортировки слиянием можно описать следующим образом:
1. Если в рассматриваемом массиве один элемент, то он уже отсортирован — алгоритм завершает работу.
2. Иначе массив разбивается на две части, которые сортируются рекурсивно.
3. После сортировки двух частей массива к ним применяется процедура слияния, которая по двум отсортированным частям получает исходный отсортированный массив.

Параллельная схема

В рамках данной работы было выполнено две реализации поставленного алгоритма: с использованием технологии MPI и с помощью технологии OpenMP. Входные данные параллельной схемы выполнения:
P - количество процессоров, n – количество упорядочиваемых значений, причем p значительно меньше n. (В данной ситуации каждый процессор содержит блок сортируемого набора данных размера n/p).
A[1..n/p] – набор блоков сортируемого набора данных.
Блоки обычно упорядочиваются в самом начале сортировки на каждом процессоре в отдельности при помощи какого-либо быстрого алгоритма (начальная стадия параллельной сортировки ). Далее, следуя схеме одноэлементного сравнения, взаимодействие пары процессоров Pi и Pi+1 для совместного упорядочения содержимого блоков Ai и Ai+1 может быть осуществлено следующим образом:
1. Разбиение оставшегося числа процессоров на пары (Pi ; Pi+1) и передача данных процессору Pi+1;
2. Выполнить слияние блоков на Pi+1 процессоре в один отсортированный блок двойного размера;
3. Если число отсортированных блоков больше 1 – переход к шагу 1; иначе – останов.

Анализ эффективности

Трудоёмкость выполнения последовательного алгоритма сортировки слияния равна О(n*log2(n)).
Теперь определим трудоёмкость параллельного алгоритма. После передачи элементов всем процессам они выполняют сортировку последовательным алгоритмом слияния. Значит трудоёмкость t1 равна
t1 = (n/p)*log2(n/p)
Определим трудоёмкость метода при слиянии массивов из процессов. Число итераций равно p-1, а в каждой итерации число перестановок равно отношению количества элементов в изначальном массиве n к используемому количеству процессов на данной итерации. На первом шаге их p, на втором p/2 и т.д. То есть трудоёмкость t2 равна
t2 = n/p + 2*n/p + ... + n = n*(2p-1)/p
Окончательная оценка алгоритма Tp равна
Tp=Tp(comm)+t1+t2=p(a+w(n/p)/b) + (n/p)*log2(n/p) + n*(2p-1)/p
Общая оценка показателя ускорения равна:
Sp = n*log2n / [p(a+w(n/p)/b) + (n/p)*log2(n/p) + n*(2p-1)/p]
Оценка эффективности:
Ep = n*log2n / p*[p(a+w(n/p)/b) + (n/p)*log2(n/p) + n*(2p-1)/p]

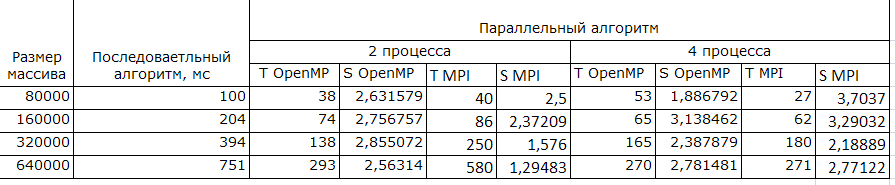
Результаты вычислительных экспериментов

Об авторах

Сагин А.А., Фетюкова А.Н., гр. 8409