Постановка задачи

Задача сортировки часто возникает при создании различных систем автоматизации обработки данных на базе ЭВМ. Под сортировкой подразумевают задачу размещения элементов неупорядоченного набора значений

в порядке монотонного возрастания (или убывания)

Для решения подобного рода задач разработано достаточно большое количество алгоритмов сортировки. Это разнообразие алгоритмов объясняется высокой трудоёмкостью решаемой задачи с одной стороны и большими объёмами входных данных с другой стороны. В итоге возникает необходимость максимально эффективно решать данную задачу обработки данных.

Существенного прироста в скорости выполнения таких задач можно добиться распараллеливанием вычислений, благо современные технологии позволяют распоряжаться одновременно несколькими вычислительными узлами. Следовательно, необходимо иметь как последовательную, так и параллельную версию алгоритма

В данной работе рассмотрены последовательный и параллельный алгоритмы быстрой сортировки, предложенный Хоара (C.A.R. Hoare).

Метод решения

Последовательный алгоритм

При общем рассмотрении алгоритма быстрой сортировки, прежде всего, следует отметить, что этот метод основывается на последовательном разделении сортируемого набора данных на блоки меньшего размера таким образом, что между значениями разных блоков обеспечивается отношение упорядоченности (для любой пары блоков все значения одного из этих блоков не превышают значений другого блока). На первой итерации метода осуществляется деление исходного набора данных на первые две части – для организации такого деления выбирается некоторый ведущий элемент и все значения набора, меньшие ведущего элемента, переносятся в первый формируемый блок, все остальные значения образуют второй блок набора. На второй итерации сортировки, описанные правила применяются рекурсивно для обоих сформированных блоков и т.д. При надлежащем выборе ведущих элементов после выполнения итераций исходный массив данных оказывается упорядоченным.

Эффективность быстрой сортировки в значительной степени определяется правильностью выбора ведущих элементов при формировании блоков. В худшем случае трудоемкость метода имеет тот же порядок сложности, что и пузырьковая сортировка. При оптимальном выборе ведущих элементов, когда разделение каждого блока происходит на равные по размеру части, трудоемкость алгоритма совпадает с быстродействием наиболее эффективных способов сортировки. В среднем случае количество операций, выполняемых алгоритмом быстрой сортировки, определяется выражением:

 

Параллельный алгоритм

Параллельное обобщение алгоритма быстрой сортировки наиболее простым способом может быть получено, если топология коммуникационной сети может быть эффективно представлена в виде N -мерного гиперкуба (т.е. p=2^N ). Пусть исходный набор данных распределен между процессорами блоками одинакового размера n/p ; результирующее расположение блоков должно соответствовать нумерации процессоров гиперкуба.
Предполагается, что вначале каждый процессор имеет часть исходных данных для сортировки. Сортировка располагаемых на процессорах блоков происходит в самом начале выполнения вычислений. Для поддержки упорядоченности в ходе вычислений процессоры должны выполнять операции слияния частей блоков, получаемых после разделения.

После окончания параллельного алгоритма сортировки каждый процессор будет содержать некоторую часть отсортированного массива так, что:
1) Каждая часть отсортирована
2) Для всех i

Для N -мерного гиперкуба алгоритм можно представить в следующем виде:
1) для i=N до 1

1.1) для каждого i-мерного куба

      ведущий процессор рассылает его средний элемент всем в i-кубе в качестве ведущего элемента (pivot)

1.2) выделяем для (i-1)-куба в этом i-кубе

1.3) каждая пара процессоров-партнеров в (i-1)-кубе обменивается данными:

     процессор с меньшим номером отдает партнеру элементы больше ведущего

     процессор с большим номером отдает партнеру элементы меньше ведущего

     на каждом из процессоров происходит слияние данных

Заметим, что на i-ой итерации, каждый из подгиперкубов будут образовывать процессоры, в битовых представлениях номеров которых различаются i-ые (слева) позиции;

После первой итерации все элементы в нижнем (N-1)-мерном кубе будут меньше, чем все элементы в верхнем (N-1)-мерном кубе. После N таких шагов массив будет отсортирован.

 

Анализ эффективности

Оценим трудоемкость рассмотренного параллельного метода. Пусть у нас имеется N - мерный гиперкуб состоящий из p=2^N процессоров, где p < n.

Эффективность параллельного метода быстрой сортировки, как и в последовательном варианте, во многом зависит от правильности выбора значений ведущих элементов. Определение общего правила для выбора этих значений представляется затруднительным. Сложность такого выбора может быть снижена, если выполнить упорядочение локальных блоков процессоров перед началом сортировки и обеспечить однородное распределение сортируемых данных между процессорами вычислительной системы.

Определим вначале вычислительную сложность алгоритма сортировки. На каждой из log_p2 итераций сортировки каждый процессор осуществляет деление блока относительно ведущего элемента, сложность этой операции составляет n/p операций (будем предполагать, что на каждой итерации сортировки каждый блок делится на равные по размеру части).

При завершении вычислений процессоры выполняет сортировку своих блоков, что может быть выполнено при использовании быстрых алгоритмов за (n/p)log₂(n/p) операций.

Таким образом, общее время вычислений параллельного алгоритма быстрой сортировки составляет:

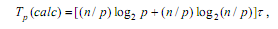
где τ есть время выполнения базовой операции перестановки.

Рассмотрим теперь сложность выполняемых коммуникационных операций. Общее количество межпроцессорных обменов для рассылки ведущего элемента на N-мерном гиперкубе может быть ограничено оценкой:

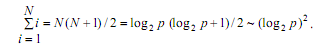
При используемых предположениях (выбор ведущих элементов осуществляется самым наилучшим образом), количество итераций алгоритма равно log₂p, а объем передаваемых данных между процессорами всегда является равным половине блока, т.е. (n/p)/2). При таких условиях, коммуникационная сложность параллельного алгоритма быстрой сортировки определяется при помощи соотношения:

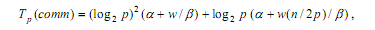
где α - латентность, β - пропускная способность сети, а w есть размер элемента набора в байтах.

С учетом всех полученных соотношений общая трудоемкость алгоритма оказывается равной:

 

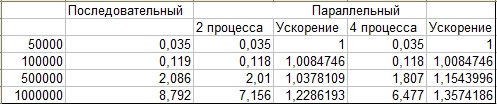
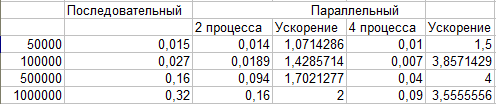
Результаты вычислительных экспериментов.

Конфигурация системы

Процессор - Intel(R) Core(TM) i5 CPU 2415M @ 2.30GHz
Оперативная память - 4 GB
Операционная система - MS Windows 7 x64
Компилятор - MS Visual Studio 2010

OpenMP

MPI

Об авторах

Работу выполнили студенты групп 8409 и 8410 Маслова З.А. и Анисимов А.С.