Постановка задачи
В данной работе необходимо:
- Реализовать параллельную программу, решающую СЛАУ методом Гаусса, с использованием библиотек MPI и OpenMp.
- Провести теоретический анализ эффективности алгоритма.
- Провести необходимые эксперименты и сделать выводы.
Схема последовательного алгоритма
Одним из самых распространенных методов решения систем линейных уравнений является метод Гаусса.
Вычисления с помощью метода Гаусса заключаются в последовательном исключении неизвестных из системы для преобразования ее к эквивалентной системе с верхней треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода.
Метод Гаусса с выбором главного элемента по всей матрице (схема полного выбора).
Прямой ход
На 1-м шаге метода среди элементов aij определяют максимальный по модулю элемент. Первое уравнение системы и уравнение с номером i1 меняют местами. Далее стандартным образом производят исключение неизвестного xi1 из всех уравнений, кроме первого.Будем называть его главным элементом 1-го шага.
Найдем величины qi1 = ai1/a11 (i = 2, 3, …, n), называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, …, n-го уравнений системы первое уравнение, умноженное соответственно на q21, q31, …, qn1. Это позволит обратить в нуль коэффициенты при x1 во всех уравнениях, кроме первого. В результате получим эквивалентную систему
a11x1 + a12x2 + a13x3 + … + a1nxn = b1
a22x2 + a23x3 + … + a2nxn = b2
a33x3 + … + a3nxn = b3
………………………………………
annxn = bn
Матрица A является верхней треугольной. На этом вычисления прямого хода заканчиваются.
Обратный ход.
Из последнего уравнения системы находим xn. Подставляя найденное значение xn в предпоследнее уравнение, получим xn–1. Осуществляя обратную подстановку, далее последовательно находим xn–1, xn–2, …, x1.
Алгоритм нахождения координаты решения по методу Гаусса заключается в следующем:
- Находим главный элемент по всей матрице (Max). Строку содержащую данный элемент принимаем за главную на текущей итерации.
- Приводим матрицу коэффициентов к треугольному виду.
- Осуществляем обратный ход и находим координаты решения по методу Гаусса.
Реализация прямого хода требует
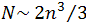
арифметических операций, а обратного –
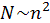
арифметических операций.
Схема параллельного алгоритма
При внимательном рассмотрении метода Гаусса можно заметить, что все вычисления сводятся к однотипным вычислительным операциям над строками матрицы коэффициентов системы линейных уравнений. Как результат, в основу параллельной реализации алгоритма Гаусса может быть положен принцип распараллеливания по данным. В качестве базовой подзадачи можно принять тогда все вычисления, связанные с обработкой одной строки матрицы A и соответствующего элемента вектора b.
Определение подзадач
Рассмотрим общую схему параллельных вычислений и возникающие при этом информационные зависимости между базовыми подзадачами.
Для выполнения прямого хода метода Гаусса необходимо осуществить (n-1) итерацию по исключению неизвестных для преобразования матрицы коэффициентов A к верхнему треугольному виду.
Выполнение итерации i, 0<=i
Далее для продолжения вычислений ведущая подзадача должна разослать свою строку матрицы A и соответствующий элемент вектора b всем остальным подзадачам с номерами k, k
При выполнении обратного хода метода Гаусса подзадачи выполняют необходимые вычисления для нахождения значения неизвестных. Как только какая-либо подзадача i, 0<=i
Масштабирование и распределение подзадач по процессорам
Выделенные базовые подзадачи характеризуются одинаковой вычислительной трудоемкостью и сбалансированным объемом передаваемых данных. В случае когда размер матрицы, описывающей систему линейных уравнений, оказывается большим, чем число доступных процессоров, базовые подзадачи можно укрупнить, объединив в рамках одной подзадачи несколько строк матрицы. Однако применение последовательной схемы разделения данных для параллельного решения систем линейных уравнений приведет к неравномерной вычислительной нагрузке процессоров: по мере исключения (на прямом ходе) или определения (на обратном ходе) неизвестных в методе Гаусса для все большей части процессоров все необходимые вычисления будут завершены и процессоры окажутся простаивающими. Возможное решение проблемы балансировки вычислений может состоять в использовании ленточной циклической схемы для распределения данных между укрупненными подзадачами. В этом случае матрица A делится на наборы (полосы) строк вида (см. рис. 1):


рис.1.
Сопоставив схему разделения данных и порядок выполнения вычислений в методе Гаусса, можно отметить, что использование циклического способа формирования полос позволяет обеспечить лучшую балансировку вычислительной нагрузки между подзадачами.
Распределение подзадач между процессорами должно учитывать характер выполняемых в методе Гаусса коммуникационных операций. Основным видом информационного взаимодействия подзадач является операция передачи данных от одного процессора всем процессорам вычислительной системы. Как результат, для эффективной реализации требуемых информационных взаимодействий между базовыми подзадачами топология сети передачи данных должны иметь структуру гиперкуба или полного графа.
Анализ эффективности
Оценим трудоемкость рассмотренного параллельного варианта метода Гаусса. Пусть, как и ранее, n есть порядок решаемой системы линейных уравнений, а p, p
Прежде всего, несложно показать, что общее время выполнения последовательного варианта метода Гаусса составляет:
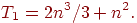
Определим теперь сложность параллельного варианта метода Гаусса. При выполнении прямого хода алгоритма на каждой итерации для выбора ведущей строки каждый процессор должен осуществить выбор максимального значения в столбце с исключаемой неизвестной в пределах своей полосы. Начальный размер полос на процессорах равен n/p, но по мере исключения неизвестных количество строк в полосах для обработки постепенно сокращается. Текущий размер полос приближенно можно оценить как (n-i)/p, где i, 0<=i
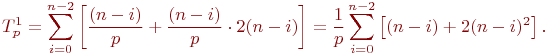
На каждой итерации обратного хода алгоритма Гаусса после рассылки вычисленного значения очередной неизвестной каждый процессор должен обновить значения правых частей для всех строк, расположенных на этом процессоре. Отсюда следует, что трудоемкость параллельного варианта обратного хода алгоритма Гаусса оценивается как величина:

Просуммировав полученные выражения, можно получить
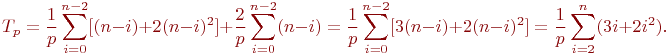
Как результат выполненного анализа, показатели ускорения и эффективности параллельного варианта метода Гаусса могут быть определены при помощи соотношений следующего вида:
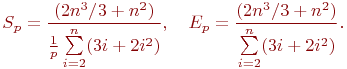
Полученные соотношения имеют достаточно сложный вид для оценивания. Вместе с тем можно показать, что сложность параллельного алгоритма имеет порядок ~(2n3/3)/p, и, тем самым, балансировка вычислительной нагрузки между процессорами в целом является достаточно равномерной.
Дополним сформированные показатели вычислительной сложности метода Гаусса оценкой затрат на выполнение операций передачи данных между процессорами. При выполнении прямого хода на каждой итерации для определения ведущей строки процессоры обмениваются локально найденными максимальными значениями в столбце с исключаемой переменной. Выполнение данного действия одновременно с определением среди собираемых величин наибольшего значения может быть обеспечено при помощи операции обобщенной редукции (функция MPI_Allreduce библиотеки MPI ). Всего для выполнения такой операции требуется log2p шагов, что с учетом количества итераций позволяет оценить время, необходимое для проведения операций редукции, при помощи следующего выражения
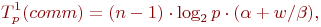
Далее также на каждой итерации прямого хода метода Гаусса выполняется рассылка выбранной ведущей строки. Сложность данной операции передачи данных:
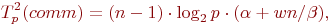
При выполнении обратного хода алгоритма Гаусса на каждой итерации осуществляется рассылка между всеми процессорами вычисленного значения очередной неизвестной. Общее время, необходимое для выполнения подобных действий, можно оценить как:
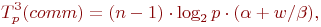
В итоге, с учетом всех полученных выражений, трудоемкость параллельного варианта метода Гаусса составляет:
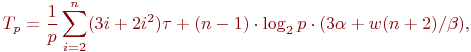
где  есть время выполнения базовой вычислительной операции.
есть время выполнения базовой вычислительной операции.
Результаты вычислительных экспериментов
Использование библиотеки MPI

Использование библиотеки OpenMP

Выводы
На основании проведенных экспериментов можно сделать следующие выводы:
OpenMP
При использовании библиотеки OpenMP ускорение имеется при любой размерности, но наибольший эффект от распараллеливание наблюдается при размерностях задач около 1500-2000, при дальнейшем росте размерности эффективность снижается.
MPI
При использовании библиотеки MPI наиболее разумной стратегией является распараллеливание на количество процессов равное количеству ядер, с противном случае наблюдается снижение производительности. Следует заметить, что при увеличении размерности задачи наблюдается рост ускорения.
Что касается сравнения этих библиотек, то следует заметить, что MPI в целом показала себя лучше чем OpenMP.
Об авторах
Комин А.В. группа 8409 Зубова М.М. группа 8410


