Умножение матриц (горизонтальное разбиение)

Постановка задачи

Требуется получить результат умножения двух квадратных матриц, элементы которых заданы случайным образом. Для решения задачи используются последовательная и параллельная версии ленточного алгоритма перемножения матриц. Параллельная версия разрабатывается на основе последовательной с использованием технологии OpenMP, что позволяется достичь ускорения при умножении матриц больших размеров. При реализации алгоритма используется разбиение перемножаемых матриц по строкам.

Метод решения

Пусть A и B – матрицы, которые необходимо перемножить, C – матрица, содержащая результат умножения. Начальные значения всех элементов матрицы C равны нулю. Алгоритм представляет собой итерационную процедуру. На каждой итерации алгоритма одна строка матрицы A умножается на одну строку матрицы B. При выполнении итерации проводится поэлементное умножение строк, что приводит к получению строки частичных результатов для матрицы С. Пример работы алгоритма представлен на рис. 1.

Параллельная схема

Пусть каждый поток будет считывать и поочередно перемножать одну строку матрицы A со всеми строками матрицы B. Таким образом, данный поток будет находить частичные результаты для одной строки матрицы C и суммировать их. В результате потоком будет получена строка матрицы C, номер которой будет таким же, как номер строки, считанной из матрицы A. Заметим, что если поделить данные между потоками таким образом, то при записи полученных строк в матрицу C гонка данных не возникает.

void ParallelMultiply(double* pAMatrix, double* pBMatrix, double* pCMatrix, int size)
{
   #pragma omp parallel for
   for (int i = 0; i < size; i++)
   {
      for (int j = 0; j < size; j++)
      {
         for (int k = 0; k < size; k++)
         {
            pCMatrix[i * size + k] += pAMatrix[i * size + j] * pBMatrix[j * size + k];
         }
      }
   }
}

Анализ эффективности

     Пусть размер матриц A, B, C равен n × n.      Рассмотрим одну итерацию алгоритма, соответствующую внешнему циклу. Чтобы получить строку частичных результатов матрицы C необходимо выполнить n операций умножения. Соответственно, для получения всех частичных результатов необходимо выполнить n * n операций умножения. При получении конечного результата для строки матрицы C нужно выполнить n * (n - 1) операций сложения.
     Таким образом, для вычисления одной строки матрицы C необходимо выполнить n * n + n * (n - 1) скалярных операций.
     Трудоемкость всего умножения матриц составляет n * (n * n + n * (n - 1)).
     Таким образом, можно получить следующие оценки:

T1 = n^2 * (2n - 1) – оценка трудоемкости решения задачи на одноядерном процессоре
Tp = (n^2 * (2n - 1)) / p – оценка трудоемкости решения задачи на p-ядерном процессоре
S = T1 / Tp = p – ускорение
E = S / p = 1 – эффективность

Результаты вычислительных экспериментов

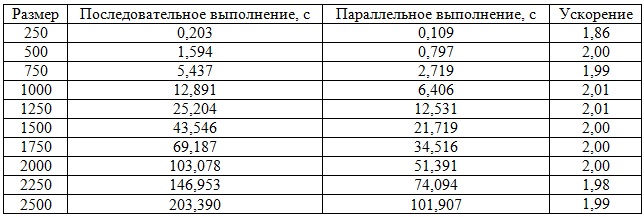
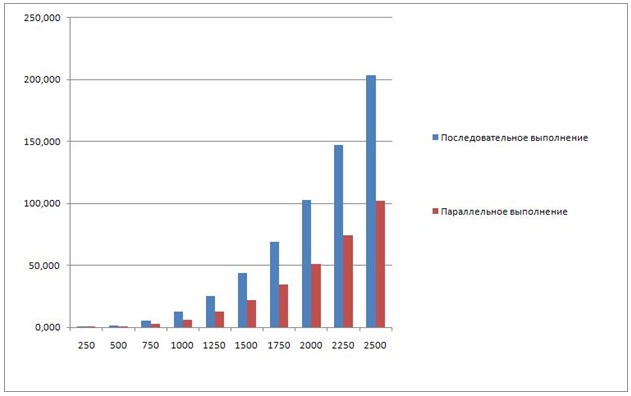
OpenMP

Intel(R) Core(TM) 2 CPU 6300 @ 1.86GHz
RAM: 1 Гб ОЗУ
Использовался стандартный компилятор, встроенный в Visual Studio 2010.
ОС: Windows XP

MPI

Inte(R) Core(TM) 2 QUAD CPU @2.40Ghz
RAM: 4 Гб ОЗУ
Использовался стандартный компилятор, встроенный в Visual Studio 2010.
ОС: Windows 7

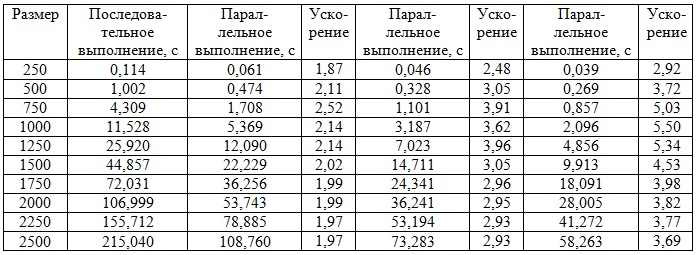
В таблице приведены данные для последовательного выполнения, а так же параллельного выполнения с использованием двух, трех и четырех процессов соответственно.

Об авторах

Студент группы 8409 - Ильичев А.С., Студент группы 8409 - Синицын А.Н.