Постановка задачи

Необходимо реализовать параллельную программу, которая решает системы линейных алгебраических уравнений (СЛАУ) методом Гаусса средствами MPI и OpenMP. Также нужно провести теоретический анализ эффективности алгоритма, провести эксперименты и сделать выводы.

Описание последовательного алгоритма

Линейное уравнение с n неизвестными x₀, x₁, …, x_n-1 может быть определено при помощи выражения a₀x₀ + a₁x₁ + ... + a_n-1x_n-1 = b где величины a₀, a₁, …, a_n-1 и b представляют собой постоянные значения.

Множество n линейных уравнений

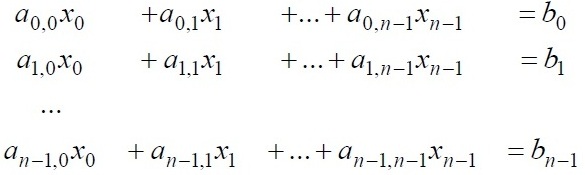
называется системой линейных уравнений или линейной системой. В матричном виде система может представлена как Ax = b где A = (a_i,j) есть вещественная матрица размера n×n, а вектора b и x состоят из n элементов.

Под задачей решения системы линейных уравнений для заданных матрицы А и вектора b обычно понимается нахождение значения вектора неизвестных x, при котором выполняются все уравнения системы.

Метод Гаусса основывается на возможности выполнения преобразований линейных уравнений, которые не меняют при этом решение рассматриваемой системы (эквивалентные преобразования). К ним относятся:

• Умножение любого из уравнений на ненулевую константу,
• Перестановка уравнений,
• Прибавление к уравнению любого другого уравнения системы.

Метод Гаусса включает последовательное выполнение двух этапов.Первый этап – прямой ход метода Гаусса – исходная система линейный уравнений приводится к верхнему треугольному виду Ux = c где матрица коэффициентов получаемой системы имеет вид

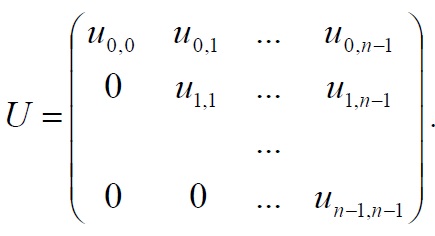
Прямой ход метода Гаусса состоит в последовательном исключении неизвестных в уравнениях решаемой системы линейных уравнений. На итерации i, 0 ≤ i < n-1, метода производится исключение неизвестной i для всех уравнений с номерами k, больших i (т.е. i< k ≤ n-1,). Для этого из этих уравнений осуществляется вычитание строки i умноженной на константу a_ki / a_ii с тем, чтобы результирующий коэффициент при неизвестной x_i в строках оказался нулевым – все необходимые вычисления могут быть определены при помощи соотношений:

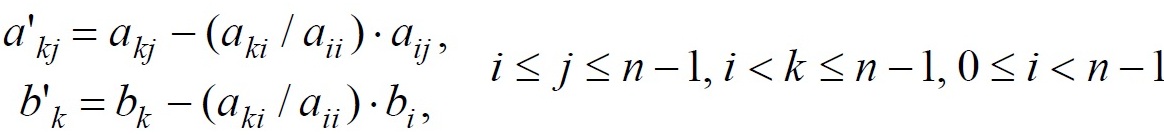
Все коэффициенты при неизвестных, расположенные ниже главной диагонали и левее столбца i, уже являются нулевыми. На i-ой итерации прямого хода метода Гаусса осуществляется обнуление коэффициентов столбца i, расположенных ниже главной диагонали, путем вычитания строки i, умноженной на нужную ненулевую константу. После проведения (n-1) подобной итерации матрица, определяющая систему линейных уравнений, становится приведенной к верхнему треугольному виду.

При выполнении прямого хода метода Гаусса строка, которая используется для исключения неизвестных, носит наименование ведущей, а диагональный элемент ведущей строки называется ведущим элементом. Выполнение вычислений является возможным только, если ведущий элемент имеет ненулевое значение. Более того, если ведущий элемент a_i,i имеет малое значение, то деление и умножение строк на этот элемент может приводить к накоплению вычислительной погрешности и вычислительной неустойчивости алгоритма.

Чтобы избежать подобной проблемы может состоять в следующем – при выполнении каждой очередной итерации прямого хода метода Гаусса следует определить коэффициент с максимальным значением по абсолютной величине в столбце, соответствующем исключаемой неизвестной, т.е.

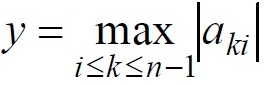
и выбрать в качестве ведущей строку, в которой этот коэффициент располагается

Вычислительная сложность прямого хода алгоритма Гаусса с выбором ведущей строки имеет порядок O(n³).

Обратный ход алгоритма Гаусса

После приведения матрицы коэффициентов к верхнему треугольному виду становится возможным определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной x_n-1, после этого из предпоследнего уравнения становится возможным определение переменной x_n-2 и тд. В общем виде, выполняемые вычисления при обратном ходе метода Гаусса могут быть представлены при помощи соотношений:

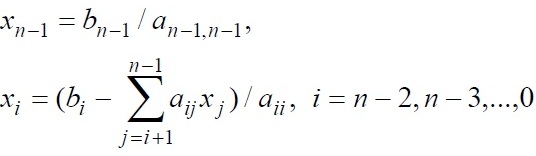
Вычислительная сложность обратного хода алгоритма Гаусса составляет O(n²).

Описание параллельного алгоритма. Выделение информационных зависимостей

Все вычисления методом Гаусса сводятся к однотипным вычислительным операциям над строками матрицы коэффициентов системы линейных уравнений. Значит в основу параллельной реализации алгоритма Гаусса может быть положен принцип распараллеливания по данным. Поэтому, в качестве базовой подзадачи можно принять все вычисления, связанные с обработкой одной строки матрицы A и соответствующего элемента вектора b.

При выполнении прямого хода метода Гаусса необходимо осуществить (n-1) итерацию по исключению неизвестных для преобразования матрицы коэффициентов A к верхнему треугольному виду.

Выполнение итерации i, 0 ≤ i < n-1, прямого хода метода Гаусса включает ряд последовательных действий. В самом начале итерации необходимо выбрать ведущую строку, которая при использовании метода главных элементов определяется поиском строки с наибольшим по абсолютной величине значением среди элементов столбца i, соответствующего исключаемой переменной x_i. Поскольку строки матрицы A распределены по подзадачам, для поиска максимального значения подзадачи с номерами k, k > i, должны обменяться своими элементами при исключаемой переменной x_i. После сбора всех необходимых данных в каждой подзадаче может быть определено, какая из подзадач содержит ведущую строку и какое значение является ведущим элементом.

Далее для продолжения вычислений ведущая подзадача должна разослать свою строку матрицы A и соответствующий элемент вектора b всем остальным подзадачам с номерами k, k > i. Получив ведущую строку, подзадачи выполняют вычитание строк, обеспечивая тем самым исключение соответствующей неизвестной x_i.

При выполнении обратного хода метода Гаусса подзадачи выполняют необходимые вычисления для нахождения значения неизвестных. Как только какая-либо подзадача i, 0 ≤ i < n-1, определяет значение своей переменной x_i, это значение должно быть разослано всем подзадачам с номерами k, k < i. Далее подзадачи подставляют полученное значение новой неизвестной и выполняют корректировку значений для элементов вектора b.

Масштабирование и распределение подзадач по процессорам

Выделенные базовые подзадачи характеризуются одинаковой вычислительной трудоемкостью и сбалансированным объемом передаваемых данных. В случае, когда размер матрицы, описывающей систему линейных уравнений, оказывается большим, чем число доступных процессоров (p < n), базовые подзадачи можно увеличить, объединив в одной подзадачи несколько строк матрицы. Применение последовательной схемы разделения данных для параллельного решения систем линейных уравнений приведет к неравномерной вычислительной нагрузке процессоров – по мере исключения или определения неизвестных в методе Гаусса для все большей части процессоров все необходимые вычисления будут завершены и процессоры окажутся простаивающими. Решение проблемы балансировки вычислений может состоять в использовании ленточной циклической схемы для распределения данных между увеличенными подзадачами. В этом случае матрица A делится на наборы (полосы) строк вида

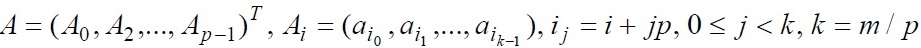
Использование циклического способа формирования полос позволяет обеспечить лучшую балансировку вычислительной нагрузки между подзадачами.

Основным видом информационного взаимодействия подзадач является операция передачи данных от одного процессора всем процессорам вычислительной системы. Как результат, для эффективной реализации требуемых информационных взаимодействий между базовыми подзадачами топология сети передачи данных должны иметь структуру гиперкуба или полного графа.

Анализ эффективности

Пусть n есть порядок решаемой системы линейных уравнений, а p, p < n, обозначает число используемых процессоров. Тогда матрица коэффициентов А имеет размер n×n и, соответственно, n/p есть размер полосы матрицы А на каждом процессоре. Общее время выполнения последовательного варианта метода Гаусса составляет:

T₁ = 2n³/3 + n²

Определим сложность параллельного варианта метода Гаусса. При выполнении прямого хода алгоритма на каждой итерации для выбора ведущей строки каждый процессор должен осуществить выбор максимального значения в столбце с исключаемой неизвестной в пределах своей полосы. Начальный размер полос на процессорах равен n/p, но по мере исключения неизвестных количество строк в полосах для обработки постепенно сокращается. Текущий размер полос приближенно можно оценить как (n-i)/p, где i, 0 ≤ i < n-1, есть номер выполняемой итерации прямого хода метода Гаусса. Далее после сбора полученных максимальных значений, определения и рассылки ведущей строки, каждый процессор должен выполнить вычитание ведущей строки из каждой строки оставшейся части строк своей полосы матрицы A. Количество элементов строки, подлежащих обработке, также сокращается при исключении неизвестных, и текущее число элементов строки для вычислений оценивается величиной (n-i). Тем самым, сложность процедуры вычитания строк оценивается как 2·(n-i) операций (перед вычитанием ведущая строка умножается на масштабирующую величину a_ik/a_ii). С учетом выполняемого количества итераций, общее число операций параллельного варианта прямого и обратного хода метода Гаусса определяется выражением:

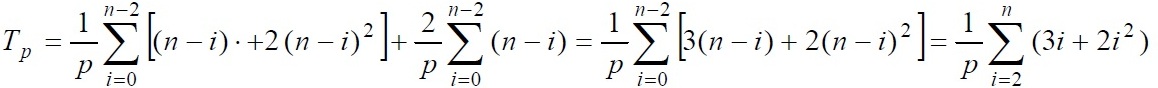
Показатели ускорения и эффективности параллельного варианта метода Гаусса могут быть определены при помощи соотношений следующего вида:

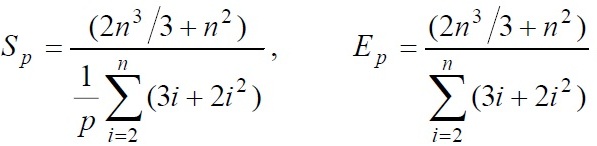
Cложность параллельного алгоритма имеет порядок ~(2n³/3)/p, тем самым, балансировка вычислительной нагрузки между процессорами в целом является достаточно равномерной. При выполнении прямого хода на каждой итерации для определения ведущей строки процессоры обмениваются локально найденными максимальными значениями в столбце с исключаемой переменной. Выполнение данного действия одновременно с определением среди собираемых величин наибольшего значения может быть обеспечено при помощи операции обобщенной редукции (функция MPI_Allreduce библиотеки MPI). Всего для выполнения такой операции требуется log₂p шагов, что с учетом количества итераций позволяет оценить время, необходимое для проведения операций редукции, при помощи следующего выражения:

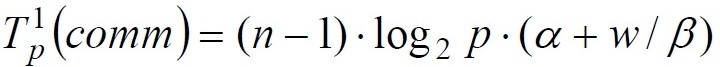
где, α – латентность сети передачи данных, β – пропускная способность сети, w – размер пересылаемого элемента данных.

На каждой итерации прямого хода метода Гаусса выполняется рассылка выбранной ведущей строки. Сложность данной операции передачи данных равна:

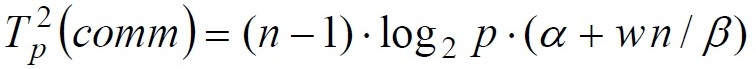
При выполнении обратного хода алгоритма Гаусса на каждой итерации осуществляется рассылка между всеми процессорами вычисленного значения очередной неизвестной. Общее время, необходимое для выполнения подобных действий, можно оценить как:

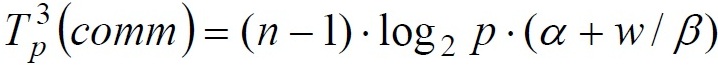
Подводя итог, с учетом всех полученных выражений, трудоемкость параллельного варианта метода Гаусса составляет:

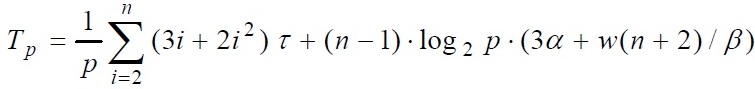
где τ есть время выполнения базовой вычислительной операции.

Эксперименты

Оборудование: Intel Core i3 M330  2.13GHz, 4 Гб ОЗУ

MPI:

Количество уравнений	1 процесс	2 процесса		4 процесса
	время(сек.)	время(сек)	Ускорение	Время(сек)	Ускорение
500	0,25	0,13	1.92	0.16	1.56
1000	2,05	1,08	1.89	1.11	1.84
1500	6,84	3,55	1.92	3.23	2.11
2000	16,17	8,48	1.90	7.81	2.07
2500	31,28	16,28	1.92	14.97	2.08
3000	54,24	27,74	1.95	25.56	2.12
3500	85,80	44,42	1.93	40.44	2.12
4000	129,50	65,44	1.97	59.06	2.19

OpenMP:

Количество уравнений	1 поток	2 потока		4 потока
	время(сек.)	время(сек)	Ускорение	Время(сек)	Ускорение
500	0,25	0,17	1,64	0,15	1.66
1000	1,8	1,1	1,63	1,3	1.38
1500	5,9	3,7	1.59	4,1	1,43
2000	14	8,7	1.60	11	1,27
2500	29,8	18	1.65	21	1,41
3000	50,9	30	1.69	36	1,41
3500	78,6	47	1.67	50	1,57
4000	123,5	68	1.81	75	1,64

 

 

Выводы

Как видно из приведённых результатов при использовании библиотеки MPI при локальных вычислениях (на одном компьютере) с числом процессов, равным числу ядер ЦП (2 ядра), выигрыш во времени происходит практически сразу и ускорение достаточно близко к идеальному, т.е. ~2. При вычислениях в 4 процесса мы получили ещё большее ускорение, так как на данном типе процессора аппаратно поддерживается 4 потока.

OpenMP в целом ускорение заметно ниже, как на 2-х потоках, так и на 4-х.

С увеличением размерности ускорение растёт как на MPI, так и на OpenMP.

 

Авторы:

Сергиенко С.Э.

Мунтян С.В.