Постановка задачи
Необходимо реализовать параллельную программу, которая решает системы линейных алгебраических уравнений (СЛАУ) методом Гаусса с помощью библиотеки MPI. Также нужно провести теоретический анализ эффективности алгоритма, провести эксперименты и сделать выводы.
Описание алгоритма
Метод Гаусса представляет собой обобщение способа подстановки и состоит в последовательном исключении неизвестных до тех пор, пока не останется одно уравнение с одним неизвестным. При этом матрица СЛАУ приводится к треугольному виду, где ниже главной диагонали располагаются только нули.
Приведение матрицы к треугольному виду называется прямым ходом метода Гаусса. Обратный ход начинается с решения последнего уравнения и заканчивается определением первого неизвестного.
Имеем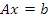 
, где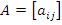 
– матрица размерности n*n, 
, 
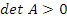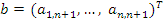. В предположении, что 
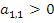, первое уравнение системы:
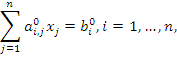
делим на коэффициент a11, в результате получаем уравнение
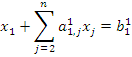
Затем из каждого из остальных уравнений вычитается первое уравнение, умноженное на соответствующий коэффициент
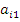
. В результате эти уравнения преобразуются к виду
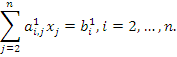
Первое неизвестное оказалось исключенным из всех уравнений, кроме первого. Далее предполагаем, что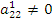 
, делим второе уравнение на 
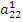и исключаем неизвестное 
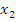из всех уравнений, начиная со второго, и т.д. В результате последовательного исключения неизвестных система уравнений преобразуется в систему уравнений с треугольной матрицей:
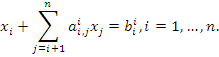
Из n-го уравнения системы определяем Xn, из (n-1)-го – Xn-1 и т.д. до X1. Совокупность таких действий называется обратным ходом метода Гаусса. Реализация прямого хода требует
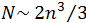
арифметических операций, а обратного –
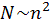
арифметических операций.
Параллельная схема
Все вычисления методом Гаусса сводятся к однотипным вычислительным операциям над строками матрицы коэффициентов системы линейных уравнений. Поэтому, в качестве базовой подзадачи можно принять все вычисления, связанные с обработкой одной строки матрицы A и соответствующего элемента вектора b. Рассмотрим общую схему параллельных вычислений и возникающие при этом информационные зависимости между базовыми подзадачами. Для выполнения прямого хода метода Гаусса необходимо осуществить (n-1) итерацию по исключению неизвестных для преобразования матрицы коэффициентов A к верхнему треугольному виду. Выполнение итерации i, 0<=i
Масштабирование и распределение подзадач по процессорам
Выделенные базовые подзадачи характеризуются одинаковой вычислительной трудоемкостью и сбалансированным объемом передаваемых данных. В случае когда размер матрицы, описывающей систему линейных уравнений, оказывается большим, чем число доступных процессоров (т.е. p
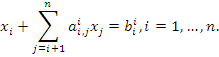
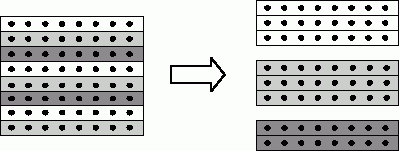
Пример использования ленточной циклической схемы разделения строк
Сопоставив схему разделения данных и порядок выполнения вычислений в методе Гаусса, можно отметить, что использование циклического способа формирования полос позволяет обеспечить лучшую балансировку вычислительной нагрузки между подзадачами.
Распределение подзадач между процессорами должно учитывать характер выполняемых в методе Гаусса коммуникационных операций. Основным видом информационного взаимодействия подзадач является операция передачи данных от одного процессора всем процессорам вычислительной системы. Как результат, для эффективной реализации требуемых информационных взаимодействий между базовыми подзадачами топология сети передачи данных должны иметь структуру гиперкуба или полного графа.
Анализ эффективности
Пусть n это порядок решаемой системы линейных уравнений, а р -число используемых процессоров.
Общее время выполнения последовательного варианта метода Гаусса составляет
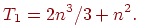
При выполнении прямого хода алгоритма на каждой итерации для выбора ведущей строки каждый процессор должен осуществить выбор максимального значения в столбце с исключаемой неизвестной в пределах своей полосы.
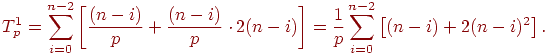
С учетом выполняемого количества итераций общее число операций параллельного варианта прямого хода метода Гаусса определяется выражением:
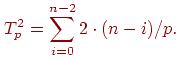
Просуммировав полученные выражения, получим
Просуммировав полученные выражения, получим
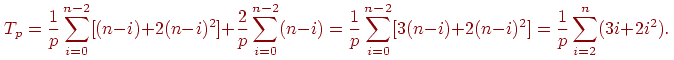
Как результат выполненного анализа, показатели ускорения и эффективности параллельного варианта метода Гаусса могут быть определены при помощи соотношений следующего вида:
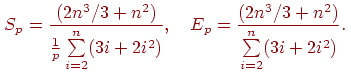
Также при выполнении прямого хода на каждой итерации выполняется рассылка массива коэффициентов. Сложность такой операции получается равной
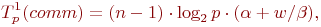
Кроме этого, на каждой итерации всем процессам рассылаются данные с номерами ведущих строки и столбца, а также номер ведущего процесса, что можно оценить
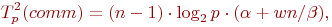
При выполнении обратного хода алгоритма Гаусса на каждой итерации осуществляется рассылка вычисленных неизвестных, что оценивается
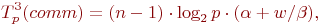
В итоге, с учетом всех полученных выражений, трудоемкость параллельного варианта метода Гаусса составляет:
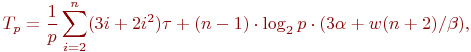
где
есть время выполнения базовой вычислительной операции.
Результаты вычислительных экспериментов
Все тесты проводились на системе следующей конфигурации:
CPU: Intel Core i5 480M 2,67GHz;
RAM: DDR3 667MHz 4 GB;
Латентность: 0,000000298 с;
Пропускная способность:1390 Mb/sec;
|
№
|
Serial
|
2 процесса
|
4 процесса
|
|
OpenMp
|
MPI
|
Ускорение OpenMP
|
Ускорение MPI
|
OpenMP
|
MPI
|
Ускорение OpenMP
|
Ускорение MPI
|
|
200
|
0,00797
|
0,019475
|
0,008108
|
0,4091399
|
0,982733103
|
0,026522
|
0,023551
|
0,300429832
|
0,338329583
|
|
400
|
0,0634
|
0,096001
|
0,038432
|
0,6604098
|
1,649666944
|
0,099227
|
0,034189
|
0,638938998
|
1,854397613
|
|
600
|
0,21449
|
0,31048
|
0,13551
|
0,6908335
|
1,582835215
|
0,2852
|
0,105632
|
0,752068724
|
2,030539988
|
|
800
|
0,55408
|
0,781284
|
0,350371
|
0,709189
|
1,581403712
|
0,708155
|
0,318244
|
0,782424752
|
1,74104775
|
|
1000
|
1,18244
|
1,460328
|
0,741041
|
0,8097058
|
1,595641807
|
1,320011
|
0,714235
|
0,895777384
|
1,655527942
|
|
1200
|
1,94314
|
2,416508
|
1,285548
|
0,8041087
|
1,511522712
|
2,240618
|
1,216061
|
0,867231719
|
1,597892704
|
|
1400
|
3,05418
|
4,234044
|
1,978672
|
0,721338
|
1,543548906
|
3,93021
|
1,932074
|
0,77710275
|
1,580776409
|
|
1600
|
4,79681
|
6,032649
|
2,928588
|
0,7951411
|
1,637924829
|
5,814725
|
2,903582
|
0,824941334
|
1,652030836
|
|
1800
|
6,75072
|
7,980592
|
4,258112
|
0,8458915
|
1,58537751
|
7,521013
|
4,172907
|
0,897580552
|
1,61774873
|
|
2000
|
9,20866
|
11,13775
|
5,655751
|
0,8267967
|
1,628193497
|
10,355349
|
5,6499
|
0,889265731
|
1,629879644
|
|
|
Serial
|
2 процесса
|
4 процесса
|
|
Теория
|
OpenMp
|
MPI
|
Теория
|
OpenMP
|
MPI
|
|
200
|
0.034671
|
0.691208
|
0.031089
|
0.041415
|
1.362569
|
0.057205
|
0.053159
|
|
400
|
0.231290
|
2.809778
|
0.207143
|
0.183384
|
5.462253
|
1.373777
|
0.604760
|
|
600
|
0.781192
|
6.433597
|
0.721566
|
0.523413
|
12.337942
|
0.861675
|
0.515147
|
|
800
|
1.793371
|
11.640583
|
1.615036
|
1.094836
|
22.028597
|
1.460269
|
1.060172
|
|
1000
|
3.224574
|
18.508657
|
3.206524
|
1.859402
|
34.573176
|
2.787145
|
2.019996
|
|
1200
|
5.662678
|
27.115739
|
5.233493
|
3.267104
|
50.010641
|
5.044962
|
3.090534
|
|
1400
|
9.027779
|
37.539749
|
8.332953
|
5.049737
|
68.379951
|
7.117178
|
4.773791
|
|
1600
|
13.402289
|
49.858606
|
12.242583
|
7.366495
|
89.720066
|
10.515629
|
6.691997
|
|
1600
|
13.402289
|
49.858606
|
12.242583
|
7.366495
|
89.720066
|
10.515629
|
6.691997
|
|
1800
|
18.895355
|
64.150232
|
17.706466
|
10.442981
|
114.069946
|
15.517708
|
10.376978
|
|
2000
|
26.011214
|
80.492545
|
24.442512
|
14.353097
|
141.468552
|
20.811915
|
13.258043
|
Выводы
Как видно из приведённых результатов при локальных вычислениях (на одном компьютере) с числом процессов, равным числу ядер ЦП (2 ядра), выигрыш во времени происходит практически сразу и ускорение достаточно близко к идеальному (идеальное ускорение на двух ядрах = 2). При вычислениях в 4 процесса на двух ядрах не получаем ощутимого положительного эффекта. Это связано с тем, что при наличии всего двух ядер, процессор является четырёхпоточным. Поэтому мы не видим ухудшения(все 4 процесса выполняются каждый в своём потоке) и улучшения (они выполняются всего на двух физических ядрах).
Из тестов становится видно, что несмотря на явный выигрыш перед теоретическими оценками, использование OpenMP не оправдывает себя, поскольку в сравнении с линейным алгоритмом, автоматически распараллеленым компилятором, этот метод явно проигрывает во времени.
Об авторе
Никитин Павел
группа 8410
