Постановка задачи

Сортировка является одной из типовых проблем обработки данных и обычно понимается как задача размещения элементов неупорядоченного набора значений


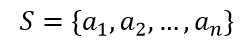
в порядке монотонного возрастания или убывания



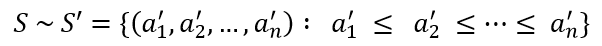
В данной работе реализован алгоритм быстрой сортировки, предложенной Хоаром (Hoare C.A.R.). Данный алгоритм относится к числу эффективных методов упорядочивания данных и широко используется в практических приложениях.

Метод решения

Алгоритм быстрой сортировки основывается на последовательном разделении сортируемого набора данных на блоки меньшего размера таким образом, что между значениями разных блоков обеспечивается отношение упорядоченности (для любой пары блоков все значения одного из этих блоков не превышают значений другого блока).

На первой итерации метода осуществляется деление исходного набора данных на первые две части – для организации такого деления выбирается некоторый ведущий элемент и все значения набора, меньшие ведущего элемента, переносятся в первый формируемый блок, все остальные значения образуют второй блок набора.

На второй итерации сортировки описанные правила применяются рекурсивно для обоих сформированных блоков и т.д.

При надлежащем выборе ведущих элементов после выполнения log2n итераций исходный массив данных оказывается упорядоченным.

Параллельная схема

Обобщенный алгоритм

В обобщенном алгоритме быстрой сортировки (HyperQuickSort algorithm) в дополнение к обычному методу быстрой сортировки предлагается конкретный способ выбора ведущих элементов. Суть предложения состоит в том, что сортировка блоков данных выполняется в самом начале выполнения вычислений. Кроме того, для поддержки упорядоченности в ходе вычислений над блоками данных выполняется операция слияния, а затем деление полученного блока двойного размера согласно ведущему элементу. Как результат, в силу упорядоченности блоков, при выполнении алгоритма быстрой сортировки в качестве ведущего элемента целесообразнее будет выбирать средний элемент какого-либо блока.

Параллельный алгоритм

Параллельное обобщение алгоритма быстрой сортировки наиболее простым способом может быть получено для случая, когда потоки параллельной программы могут быть организованы в виде N-мерного гиперкуба (т.е. количество вычислительных элементов p = 2^N). Пусть, как и ранее, исходный набор данных логически разделен на 2p блоков одинакового размера n/2p. Тогда блоки данных образуют (N+1)-мерный гиперкуб. Возможный способ выполнения первой итерации параллельного метода при таких условиях может состоять в следующем:

1) выбрать каким – либо образом ведущий элемент (например, в качестве ведущего элемента можно взять среднеарифметическое элементов, расположенных на выбранном ведущем блоке);

2) сформировать пары блоков, для которых необходимо выполнить взаимообмен данными на данной итерации алгоритма: пары образуют блоки, для которых битовое представление номеров отличается только в позиции (N+1);

3) для каждой пары блоков определить вычислительный элемент, который будет выполнять необходимые операции;

4) параллельно выполнить операцию «сравнить и разделить» над всеми парами блоков, в результате такого обмена в блоках, для которых в битовом представлении номера бит позиции N+1 равен 0, должны оказаться части блоков со значениями, меньшими ведущего элемента; блоки с номерами, в которых бит N+1 равен 1, должны собрать, соответственно, все значении данных, превышающие значение ведущего элемента.

В результате выполнения такой итерации сортировки исходный набор оказывается разделенным на две части, одна из которых (со значениями меньшими, чем значение ведущего элемента) располагается в блоках данных, в битовом представлении номеров которых бит N+1 равен 0. Таких блоков всего p и, таким образом, исходный (N+1)–мерный гиперкуб также оказывается разделенным на два гиперкуба размерности N. К этим подгиперкубам, в свою очередь, может быть параллельно применена описанная выше процедура. После (N+1)–кратного повторения подобных итераций для завершения сортировки достаточно упорядочить полученные блоки данных, каждый вычислительный элемент упорядочивает 2 блока.

Анализ эффективности

Эффективность быстрой сортировки в значительной степени определяется правильностью выбора ведущих элементов при формировании блоков.

В среднем случае время выполнения алгоритма быстрой сортировки, определяется выражением


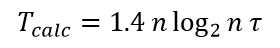
Время на обращение к оперативной памяти составляет



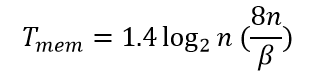
Таким образом, общее время выполнения последовательного алгоритма быстрой сортировки может быть определено при помощи выражения

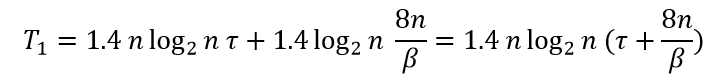
Обобщенный алгоритм

На каждой итерации метода выполняется операция слияния блоков.

Кроме того, на каждой итерации метода создаются две параллельные секции: одна для выбора ведущих элементов, вторая для выполнения слияния блоков.

Трудоемкость обобщенного алгоритма быстрой сортировки может быть выражена при помощи соотношения следующего вида


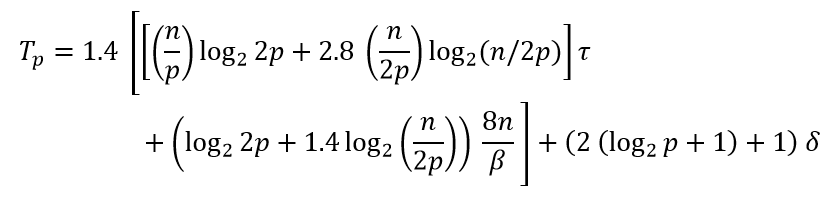
где β – пропускная способность сети.

Параллельный алгоритм

Эффективность параллельного метода быстрой сортировки, как и в последовательном варианте, во многом зависит от правильности выбора значений ведущих элементов.

Определим вычислительную сложность алгоритма сортировки. На каждой из log2(2p) итераций сортировки каждый поток осуществляет операцию «сравнить и разделить» над парой блоков в соответствии со значением ведущего элемента.

Сложность этой операции составляет n/p операций.

При завершении вычислений потоки выполняют сортировку двух блоков, что может быть выполнено при использовании быстрых алгоритмов за следующее число операций



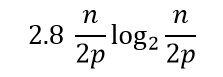
Таким образом, общее время вычислений параллельного алгоритма быстрой сортировки составляет



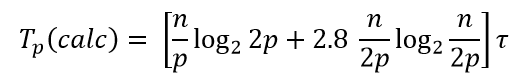
где τ есть время выполнения базовой операции перестановки.


Затраты на считывание необходимых данных из оперативной памяти в кэш составляют:



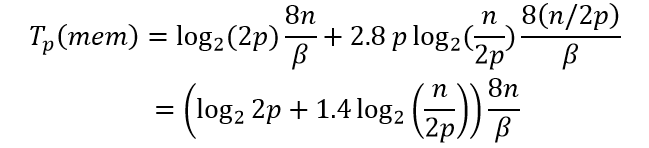
Тогда общая трудоемкость алгоритма оказывается равной:



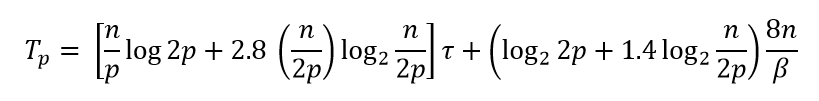
Кроме того, необходимо учесть накладные расходы на организацию параллельности, т.е.

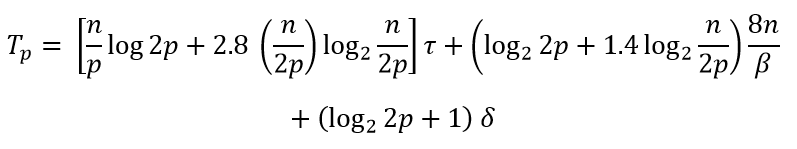
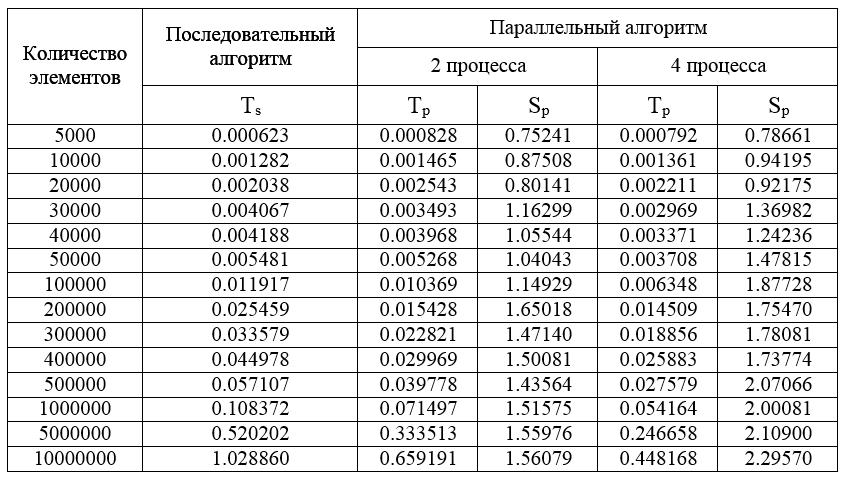
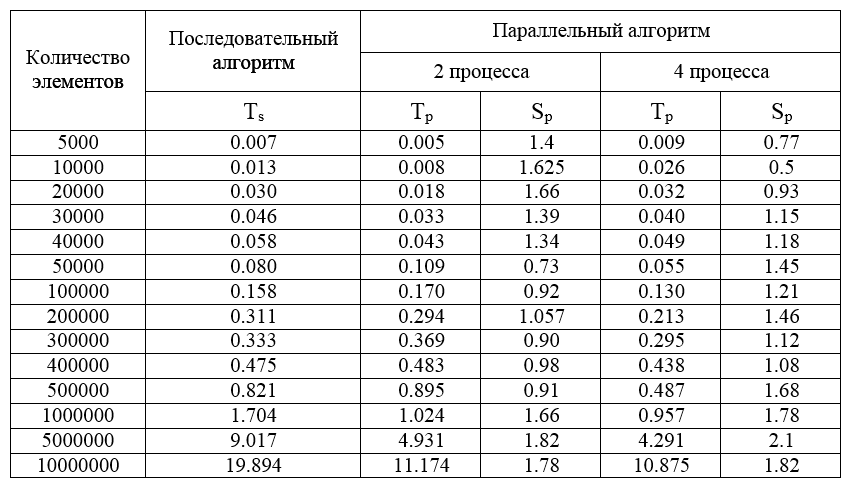
Результаты вычислительных экспериментов

Компьютер: Intel Core i7 3610QM 2.3 GHz, 6 Гб ОЗУ
Операционная система - MS Windows 8 Professional x64
Компилятор - MS Visual Studio 2010
Скорость обмена между процессами - 882028666 байт/c
Время выполнения базовой операции перестановки - 10 нс
Размер элемента набора - 8 байт (double)

MPI

OpenMP

Авторы

Артемьева Е. И., гр. 8409 и Курагина А. И., гр. 8410