Наболее трудоёмкими с точки зрения времени выполнения являются шаги 2 и 3, то есть вычисление оценок констант Липшица μ_v и характеристик интервалов R_i . На каждом из этих шагов распараллеливание реализовано схожим образом, поэтому рассмотрим в качестве примера  вычисление характеристик R_i для каждого интервала (x_i-1,x_i ), 1≤i≤k+1.

     В общем виде R_i есть некоторая функция R(x_i, x_i-1, z_i, z_i-1, μ_v), где x_i, x_i-1 – координаты границ интервала, z_i, z_i-1 – значения целевой функции в этих точках, а μ_v – нижняя оценка константы Липшица для функции либо одного из ограничений. Таким образом, вычисления значений характеристики R_i происходят для каждого интервала независимо. Это позволяет применить достаточно простую схему распараллеливания – разделение всей области поиска минимума (0,1) на несколько неперекрывающихся подобластей

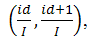
где id – номер потока, а I – общее число потоков.

     После вычисления характеристик R_i  для всех интервалов (x_i-1, x_i) ), 1≤i≤k+1 необходимо найти интервал с максимальной характеристикой. Поиск происходит также параллельно, то есть каждый поток выбирает на своей подобласти интервал с максимальной характеристикой, после чего уже из этих нескольких интервалов выбирается искомый.

К содержанию