Предположим, что необходимо найти кратчайший путь между двумя точками из множества, в случае, когда путь проходит через промежуточные точки, расстояния между которыми известно.

Пример: Доставить груз из одной части города в другую за наименьшее время.

При построении модели данной задачи, граф получается неориентированным, взвешенным.

Такой граф можно описать с помощью матрицы:

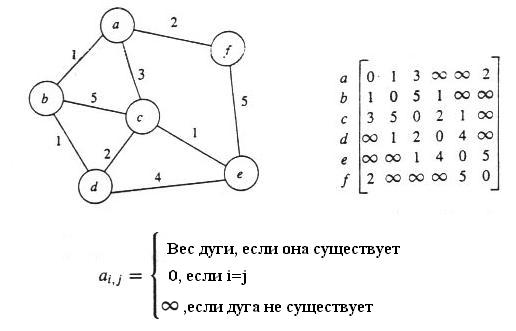
Рассмотрим взвешенный граф G = ( V ,E ,w),

где V - множество вершин графа, E - множество дуг, и w(i,j) - вес дуги соединяющей вершины i и j.

Рассмотрим подмножество {v1, v2, ... ,vk}, k<=n. Для любой пары вершин, рассмотрим все пути, промежуточные вершины которых принадлежат мн-ву {v1, v2, ... ,vk}. Пусть pk(i,j) есть кратчайший путь из них, и пусть dk(i,j) - вес этого пути. Если вершина Vk не принадлежит кратчайшему пути, то pk(i,j) = pk-1(i,j). Однако, если вершина Vk принадлежит кратчайшему пути, то мы можем разбить кратчайший путь на два пути: Vi ->Vk и Vk -> Vj. Таким образом dk(i,j) = dk-1(i,k) + dk-1(k,j). Следовательно длина кратчайшего пути вычисляется следующим образом:

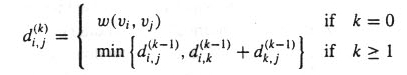
Таким образом, длина кратчайшего пути из вершины Vi в Vj есть dn(i,j). В итоге, решением задачи будет матрица Dn = (dn(i,j)).

Реализация последовательного алгоритма.

int **d,*dco,*dce;

d=(int**)new int[size];

for (k=0;k<size;++k){
  dco=d[k];
  for (i=0;i<size;++i){
   dce=d[i];
   for (j=0;j<size;++j)
    if (dce[j]>dce[k]+dco[j])
     dce[j]=dce[k]+dco[j];
  };
 };