Дифференциальные уравнения в частных производных представляют собой широко применяемый математический аппарат при разработке моделей в самых разных областях науки и техники. К сожалению, явное решение этих уравнений в аналитическом виде оказывается возможным только в частных простых случаях, и, как результат, возможность анализа математических моделей, построенных на основе дифференциальных уравнений, обеспечивается при помощи приближенных численных методов решения. Объем выполняемых при этом вычислений обычно является значительным и использование высокопроизводительных вычислительных систем является традиционным для данной области вычислительной математики.

        Рассмотрим в качестве примера проблему численного решения задачи Дирихле для уравнения Пуассона, определяемую как задачу нахождения функции u=u(x,y), удовлетворяющей в области определения  уравнению:

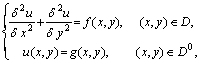
        и принимающей значения g(x,y) на границе области (f и g являются функциями, задаваемыми при постановке задачи). В качестве области задания D функции u=u(x,y), далее будет использоваться единичный квадрат.

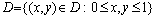
        Необходимо создать программный комплекс, реализующий метод Гаусса-Зейделя (два варианта распараллеливания) для решения задачи Дирихле для уравнения Пуассона и выполнить сравнение времени работы алгоритмов.