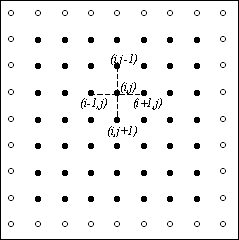Одним из наиболее распространенных
подходов численного решения дифференциальных уравнений является метод конечных
разностей (метод сеток). Следуя этому подходу, область решения
представляется в виде дискретного (как правило, равномерного) набора (сетки)
точек (узлов). Так, например, прямоугольная сетка в области может быть
задана в виде:
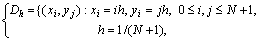
Обозначим оцениваемую при подобном
дискретном представлении аппроксимацию функции u(x,y) в точках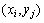 
через 
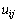. Тогда,
используя пятиточечный шаблон для вычисления значений производных, уравнение
Пуассона может быть представлено в конечно-разностной форме:
.
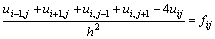Данное уравнение может быть разрешено
относительно .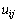
.
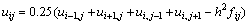Данный результат служит основой для
построения различных итерационных схем решения задачи Дирихле, в которых в
начале вычислений формируется некоторое приближение для значений 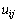, а затем
эти значения последовательно уточняются в соответствии с приведенным
соотношением. Так, например, метод Гаусса-Зейделя для проведения итераций
уточнения использует правило:
.
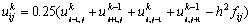Последовательность решений,
получаемых методом сеток, равномерно сходится к решению задачи Дирихле.
