Сложность проведения поиска в ширину из одной вершины составляет O(m), где m — число рёбер в компоненте сильной связности этой вершины. Для облегчения расчётов примем за m число рёбер во всём графе. Тогда время расчёта для всего графа составляет nαm, где n – число вершин в графе. Предполагая, что вершины распределяются по процессам строго поровну, получаем время работы на p процессорах .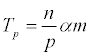

Осуществляемая при параллелизации коммуникация состоит из рассылки исходных данных всем процессам в начале (Broadcast) и сборки частичных результатов в конце (Gather). Размер рассылаемых данных пропорционален 2n+m, размер принимаемых — kn (k — размер структуры article_metrics в реализации). Таким образом время передачи данных (с учётом полной латентности l) .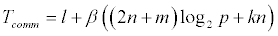

В результате ускорение будет составлять:

А эффективность:.

Видно, что эффективность увеличивается при увеличении размера графа и уменьшается при увеличении числа потоков.

Следует заметить, однако, что эти оценки применимы только в случае, когда всем процессам достаётся одинаковый размер работы. Поскольку граф может быть неравномерным, то какой-то из процессов будет работать дольше остальных, вследствие чего ускорение будет определяться временем работы этого процесса.