Пусть G есть граф G=(V,R) ,
для которого набор вершин ν ,1≤ i ≤n , задается множеством V, а список дуг графа
r_j = (v_sj,v_tj) , 1≤j≤m определяется множеством R. В общем случае дугам графа могут приписываться некоторые числовые характеристики (веса) , w _j, 1≤j≤m (взвешенный граф).
Представление достаточно плотных графов, для которых почти все вершины соединены между собой дугами (т.е m ~n²), может быть эффективно обеспечено при помощи матрицы смежности A=(a_ij) , 1≤ i, j≤n
ненулевые значения элементов которой соответствуют дугам графа

a_ij =

w (v_i,v_j), если (v_i,v_j) ɛ R;
0, если i=j;
∞ , иначе

(для обозначения отсутствия ребра между вершинами в матрице смежности на соответствующей позиции используется знак бесконечности, при вычислениях знак бесконечности может быть заменен, например, на любое отрицательное число).

Пример:



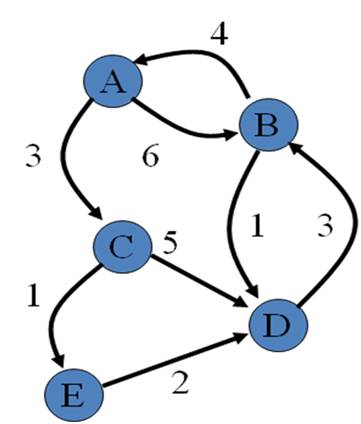
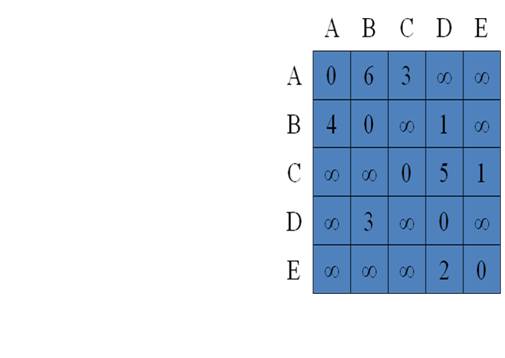
В данной лабораторной работе рассматривается способ параллельной реализации алгоритма на графах на примере задачи поиска кратчайших путей между всеми парами пунктов назначения. Задача состоит в том, что для имеющегося графа G требуется найти минимальные длины путей между каждой парой вершин графа. В качестве практического примера можно привести задачу составления маршрута движения транспорта между различными городами при заданном расстоянии между населенными пунктами и другие подобные задачи.
В качестве метода, решающего задачу поиска кратчайших путей между всеми парами пунктов назначения, далее используется алгоритм Флойда (Floyd). Граф будем полагать ориентированным, т.е., если из вершины i есть ребро в вершину j, то из этого не следует наличие ребра из j в i. В случае, если вершины все же соединены взаимообратными ребрами, то веса, приписанные им, могут не совпадать. Задача состоит в том, что для имеющегося графа G требуется найти минимальные длины путей между каждой парой вершин графа. В качестве практического примера можно привести задачу составления маршрута движения транспорта между различными городами при заданном расстоянии между населенными пунктами и другие подобные задачи.