Последовательный алгоритм Флойда.
Алгоритм Флойда находит кратчайшие пути между любыми двумя узлами сети. В этом алгоритме сеть представлена в виде квадратной матрицы с n строками и n столбцами. Элемент (i, j) равен расстоянию d_ij от узла i к узлу j, которое имеет конечное значение, если существует дуга (i, j), и равен бесконечности в противном случае.
Покажем сначала основную идею метода Флойда. Пусть есть три узла i, j и k и заданы расстояния между ними. Если выполняется неравенство d_ij + d_jk < d_ik, то целесообразно заменить путь i -> k путем i -> j -> k. Такая замена (далее ее будем условно называть треугольным оператором) выполняется систематически в процессе выполнения алгоритма Флойда.

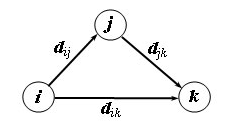
Треугольный оператор.

Последовательный алгоритм Флойда

for (k = 0; k < n; k++)
for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
D[i, j] = min(D[i, j], D[i, k] + D[k, j]);

Основной шаг k. Задаем строку k и столбец k как ведущую строку и ведущий столбец. Над матрицей D выполняется n итераций. После k-й итерации D_ij содержит значение наименьшей длины пути из вершины i в вершину j, причем путь не проходит через вершины с номерами большими k. Вычисление на k-ой итерации выполняется по формуле: min{D[i, j], D[i, k] + D[k,j]}(Рассматриваем возможность применения треугольного оператора ко всем элементам матрицы).
Для вычисления проводится сравнение величины D_ij^k-1 (то есть стоимость пути от вершины i к вершине j без участия вершины k или другой вершины с более высоким номером) с величиной D_ik^k-1+D_kj^k-1 (стоимость пути от вершины i к вершине k плюс стоимость пути от вершины k до вершины j). Если путь через вершину k “дешевле”, чем D_ij^k-1, то величина D_ij^k изменяется.

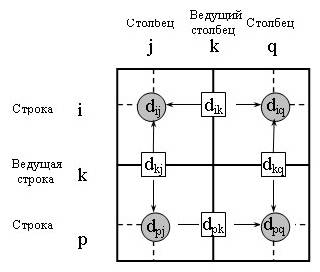
Иллюстрация метода Флойда.