Как следует из общей схемы алгоритма Флойда, основная вычислительная нагрузка при решении задачи поиска кратчайших путей состоит в выполнении операции выбора минимальных значений. Данная операция является достаточно простой, и ее распараллеливание не приведет к заметному ускорению вычислений. Более эффективный способ организации параллельных вычислений может состоять в одновременном выполнении нескольких операций обновления значений матрицы D.


Выделение информационных зависимостей.

Выполнение вычислений в подзадачах становится возможным только тогда, когда каждая подзадача (i, j) содержит необходимые для расчетов элементы D_ij, D_ik, D_kj матрицы D. Для исключения дублирования данных разместим в подзадаче (i, j) единственный элемент D_ij, тогда получение всех остальных необходимых значений может быть обеспечено только при помощи передачи данных. Таким образом, каждый элемент D_kj строки k матрицы D должен быть передан всем подзадачам (k, j) 1≤j≤n, а каждый элемент D_ik столбца k матрицы D должен быть передан всем подзадачам (i,k) 1≤i≤n.

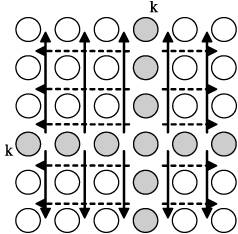
Информационная зависимость базовых подзадач (стрелками показаны направления обмена значениями на итерации k).
Масштабирование и распределение подзадач по процессорам.

Как правило, число доступных процессоров p существенно меньше, чем число базовых задач n² (p<< n²). Возможный способ укрупнения вычислений состоит в использовании ленточной схемы разбиения матрицы D – такой подход соответствует объединению в рамках одной базовой подзадачи вычислений, связанных с обновлением элементов одной или нескольких строк (горизонтальное разбиение) или столбцов (вертикальное разбиение) матрицы.
При таком способе разбиения данных на каждой итерации алгоритма Флойда потребуется передавать между подзадачами только элементы одной из строк матрицы D. Для оптимального выполнения подобной коммуникационной операции топология сети должна обеспечивать эффективное представление структуры сети передачи данных в виде гиперкуба или полного графа.