Постановка задачи
Имеется система линейных уравнений Ax=b. Требуется, используя библиотеку MPI, реализовать многопоточное приложение, вычисляющее решение данной системы с помощью метода Гаусса.
Метод решения

Метод Гаусса основывается на возможности выполнения преобразований линейных уравнений, которые не меняют при этом решения рассматриваемой системы (такие преобразования носят наименование эквивалентных). К числу таких преобразований относятся:

• умножение любого из уравнений на ненулевую константу;
• перестановка уравнений;
• прибавление к уравнению любого другого уравнения системы.

Метод Гаусса включает последовательное выполнение двух этапов. На первом этапе – прямой ход метода Гаусса – исходная система линейных уравнений при помощи последовательного исключения неизвестных приводится к верхнему треугольному виду

Ux=c, 

где матрица коэффициентов получаемой системы имеет вид  

На обратном ходе метода Гаусса (второй этап алгоритма) осуществляется определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной x_n-1, после этого из предпоследнего уравнения становится возможным определение переменной x_n-2 и т.д.

Параллельная схема

При внимательном рассмотрении метода Гаусса можно заметить, что все вычисления сводятся к однотипным вычислительным операциям над строками матрицы коэффициентов системы линейных уравнений. Как результат, в основу параллельной реализации алгоритма Гаусса может быть положен принцип распараллеливания по данным. В качестве базовой подзадачи можно принять тогда все вычисления, связанные с обработкой одной строки матрицы A и соответствующего элемента вектора b.

Для выполнения прямого хода метода Гаусса необходимо осуществить (n-1) итерацию по исключению неизвестных для преобразования матрицы коэффициентов A к верхнему треугольному виду. Прежде всего, в самом начале итерации необходимо выбрать ведущую строку, которая при использовании метода главных элементов определяется поиском строки с наибольшим по абсолютной величине значением среди элементов столбца i, соответствующего исключаемой переменной x_i. Поскольку строки матрицы A распределены по подзадачам, для поиска максимального значения подзадачи с номерами k, ki. После сбора всех необходимых данных в каждой подзадаче может быть определено, какая из подзадач содержит ведущую строку и какое значение является ведущим элементом.

Далее для продолжения вычислений ведущая подзадача должна разослать свою строку матрицы A и соответствующий элемент вектора b всем остальным подзадачам с номерами k, ki.

При выполнении обратного хода метода Гаусса подзадачи выполняют необходимые вычисления для нахождения значения неизвестных. Как только какая-либо подзадача i, 0ii, это значение должно быть разослано всем подзадачам с номерами k, k

Анализ эффективности

Оценим трудоемкость рассмотренного параллельного варианта метода Гаусса. Пусть n есть порядок решаемой системы линейных уравнений, а p, pС учетом выполняемого количества итераций общее число операций параллельного варианта прямого хода метода Гаусса определяется выражением:  

 

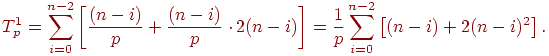
Трудоемкость параллельного варианта обратного хода алгоритма Гаусса оценивается как величина:

Просуммировав полученные выражения, можно получить:

При выполнении прямого хода на каждой итерации для определения ведущей строки процессоры обмениваются локально найденными максимальными значениями в столбце с исключаемой переменной. Всего это время занимает:

 где,  – латентность сети передачи данных, β – пропускная способность сети, w – размер пересылаемого элемента данных. Далее также на каждой итерации прямого хода метода Гаусса выполняется рассылка выбранной ведущей строки. Сложность данной операции передачи данных:

Общее время, необходимое для выполнения обратного хода, можно оценить как:

В итоге, с учетом всех полученных выражений, трудоемкость параллельного варианта метода Гаусса составляет:

где τ есть время выполнения базовой вычислительной операции.

 

Демонстрация  
Результаты вычислительных экспериментов

Конфигурация: Intel Core2 T5250 (1.5GHz), 2.00GB RAM.

Размер системы	Время выполнения (послед)	Время выполнения (паралл)	Ускорение	Время выполнения(теор)
250	0.109	0.156	0.698	0.031
500	0.563	0.578	0.974	0.246
750	1.812	1.453	1.247	0.828
1000	4.25	2.969	1.431	1.96
1250	8.253	5.313	1.553	3.824
1500	14.437	8.656	1.667	6.604
2000	33.609	19.094	1.76	15.643
2500	64.985	36.297	1.79	30.538

 Теоретическое время выполнения было посчитано с параметрами, которые получены практическим путем:

a=3.53*10^(-6);  b=6.45*10^7

Об авторах Работу выполнил: Муравьев Александр, группа 8410.