|
Умножение матрицы A размера m×n и
матрицы B размера n×l приводит к получению матрицы С размера m×l,
каждый элемент которой определяется в соответствии с выражением:
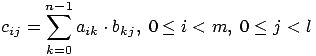 |
(1.1)
|
Как следует из (1.1), каждый элемент результирующей
матрицы С есть скалярное произведение
соответствующих строки матрицы A и
столбца матрицы B:
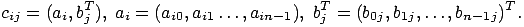 |
(1.2)
|
Этот алгоритм предполагает выполнение m·n·l операций умножения и столько же операций
сложения элементов исходных матриц. При умножении квадратных матриц
размера n×n количество выполненных
операций имеет порядок O(n3).
Известны последовательные алгоритмы умножения
матриц, обладающие меньшей вычислительной сложностью
(например, алгоритм Страссена (Strassen’s
algorithm)), но эти алгоритмы требуют больших усилий для их
освоения, и поэтому в данной лекции при разработке параллельных
методов в качестве основы будет использоваться приведенный выше
последовательный алгоритм. Также будем предполагать далее, что все
матрицы являются квадратными и имеют размер n×n. |



