Блочное разбиение матриц

При построении параллельных способов выполнения матричного умножения наряду с рассмотрением матриц в виде наборов строк и столбцов широко используется блочное представление матриц. Рассмотрим более подробно данный способ организации вычислений. При таком способе разделения данных исходные матрицы А, В и результирующая матрица С представляются в виде наборов блоков. Для более простого изложения следующего материала будем предполагать далее, что все матрицы являются квадратными размера n×n, количество блоков по горизонтали и вертикали одинаково и равно q (т.е. размер всех блоков равен k×k, k=n/q). При таком представлении данных операция матричного умножения матриц А и B в блочном виде может быть представлена так:

где каждый блок C_ij матрицы C определяется в соответствии с выражением

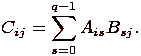
При блочном разбиении данных для определения базовых подзадач естественным представляется взять за основу вычисления, выполняемые над матричными блоками. С учетом сказанного определим базовую подзадачу как процедуру вычисления всех элементов одного из блоков матрицы С.

Для выполнения всех необходимых вычислений базовым подзадачам должны быть доступны соответствующие наборы строк матрицы A и столбцов матрицы B. Размещение всех требуемых данных в каждой подзадаче неизбежно приведет к дублированию и к значительному росту объема используемой памяти. Как результат, вычисления должны быть организованы таким образом, чтобы в каждый текущий момент времени подзадачи содержали лишь часть необходимых для проведения расчетов данных, а доступ к остальной части данных обеспечивался бы при помощи передачи данных между процессорами.