Постановка задачи

Гравитационная задача N точек является концептуальной проблемой гравитационной динамики сэра Исаака Ньютона. Наблюдение искривленных траекторий составляют физически измеримую суть гравитации; собственно гравитация не проявляет себя никаким иным образом. Вопрос "что является первопричиной тяготения" окажется содержательным, когда будут обнаружены иные способы измерения гравитации.

Гравитационная задача N тел формулируется следующим образом. В пустоте находится N материальных точек, массы которых известны {mi}. Пусть по-парное взаимодействующие точек подчинено закону тяготения Ньютона, и пусть силы гравитации аддитивны. Пусть известны начальные на момент времени t=0 положения и скорости каждой точки ri|t =0 = ri0, vi|t =0 = vi0. Требуется найти положения точек для всех последующих моментов времени.

Эволюция системы N гравитирующих тел(материальных точек) описывается следующей системой уравнений:

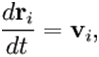
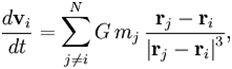
Где 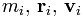 — масса, радиус-вектор и скорость i-го тела соответственно (i изменяется от 1 до N), G — гравитационная постоянная. Массы тел, а также положения и скорости в начальный момент времени считаются известными. Необходимо найти положения и скорости всех частиц в произвольный момент времени.

Параллельная схема

Используем для оценки времени передачи сообщений модель, предложенную Хокни (Hockney), в которой трудоемкость операции коммуникации между узлами вычислительной системы оценивается в соответствии с выражением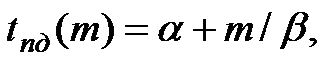

где α есть латентность сети передачи данных, m  есть размер передаваемого сообщения в байтах, а β обозначает пропускную способность сети.  Длительность выполнения операции сбора данных для первого метода реализации может быть выражена как: 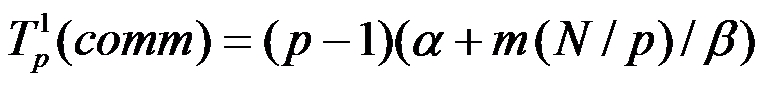. Показатель ускорения в этом случае

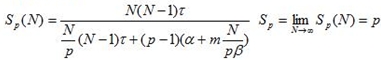
Демонстрация

Число частиц N системы разбивается на количество узлов по n_i в зависимости от расположения частиц. По мере эволюции системы, частицы переаллоцируются по узлам. Вычисления реализованы по принципу Nonblocking Pipeline – каждый процесс получает данные от процесса слева и посылает их процессу справа. Пока данные пересылаются, вычисления на ранее полученных данных не останавливаются.

Результаты экспериментов

На двухпроцессорной машине ускорение приближено к 2, что согласуется с теорией

Выполнил: Бовыкин Максим, 8409