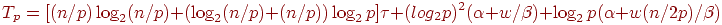Оценим трудоемкость рассмотренного параллельного метода. Пусть у нас имеется N-мерный гиперкуб, состоящий из p=2^N процессоров, где p < n.

Эффективность параллельного метода быстрой сортировки, как и в последовательном варианте, во многом зависит от правильности выбора значений ведущих элементов. Определение общего правила для выбора этих значений представляется затруднительным. Сложность такого выбора может быть снижена, если выполнить упорядочение локальных блоков процессоров перед началом сортировки и обеспечить однородное распределение сортируемых данных между процессорами вычислительной системы.

Определим вначале вычислительную сложность алгоритма сортировки.

После разбиения данных каждый процессор выполняет сортировку своего блока, что может быть выполнено при использовании быстрых алгоритмов за (n/p)log₂ (n/p) операций. На каждой из log₂p итераций в гиперкубе  каждый процессор осуществляет деление блока относительно ведущего элемента; поскольку блок упорядочен и можно применить бинарный поиск, сложность этой операции составляет log₂(n/p) (будем предполагать, что на каждой итерации сортировки каждый блок делится на равные по размеру части). На каждой итерации метода выполняется операция слияния частей блоков размером n/2p, что суммарно составляет не более n/p операций.

Таким образом, общее время вычислений параллельного алгоритма быстрой сортировки составляет

где τ есть время выполнения базовой операции перестановки.

Рассмотрим теперь сложность выполняемых коммуникационных операций. Общее количество межпроцессорных обменов для рассылки ведущего элемента на N-мерном гиперкубе может быть ограничено оценкой

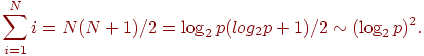
При используемых предположениях (выбор ведущих элементов осуществляется наилучшим образом) количество итераций алгоритма равно log2p, а объем передаваемых данных между процессорами всегда равен половине блока, т.е. величине (n/p)/2. При таких условиях коммуникационная сложность параллельного алгоритма быстрой сортировки определяется при помощи соотношения:

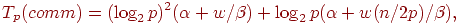
где  – латентность, β – пропускная способность сети, а w есть размер элемента набора в байтах.

С учетом всех полученных соотношений общая трудоемкость алгоритма оказывается равной