Задача об оптимальном каркасе и алгоритм Прима

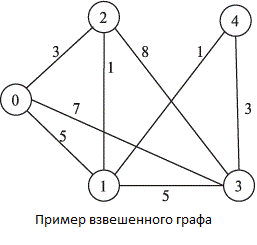
Задача об оптимальном каркасе (стягивающем дереве) состоит в следующем. Дан обыкновенный граф G=(V,E) и весовая функция на множестве ребер w: V -> R. Вес множества X, являющегося подмножеством E, определяется как сумма весов составляющих его ребер. Требуется в графе G найти каркас минимального веса. Обычно рассматривают задачу на минимум, но это не существенно - она преобразуется в задачу на максимум, если заменить функцию w на -w. Будем предполагать, что граф G связен, так что решением задачи всегда будет дерево. Для решения задачи об оптимальном каркасе известно несколько алгоритмов. Рассмотрим один из них - алгоритм Прима.

В алгоритме Прима на каждом шаге рассматривается частичное решение задачи, представляющее собой дерево. Вначале это дерево состоит из единственной вершины, в качестве которой может быть выбрана любая вершина графа. Затем к дереву последовательно добавляются ребра и вершины, пока не получится остовное дерево, т.е. каркас. Для того чтобы из текущего дерева при добавлении нового ребра опять получилось дерево, это новое ребро должно соединять вершину дерева с вершиной, еще не принадлежащей дереву. Такие ребра будем называть подходящими относительно рассматриваемого дерева. В алгоритме Прима применяется следующее правило выбора: на каждом шаге из всех подходящих ребер выбирается ребро наименьшего веса. Это ребро вместе с одной новой вершиной добавляется к дереву. Если обозначить через U и F множества вершин и ребер строящегося дерева, то алгоритм Прима можно представить следующим образом:

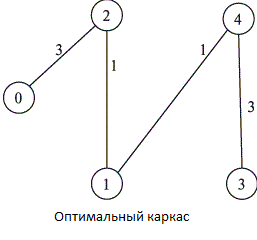
U := {a}, где а - произвольная вершина графа
F := "Пустое множество"
W := V - {a}
while W непусто do

1. найти ребро наименьшего веса e=(x, y) среди всех таких ребер, у которых х принадлежит U, а y принадлежит W
   
2. F := F + {e}
   
3. U := U + {y}
   
4. W := W - {y}

Параллельный алгоритм Прима

Итерации метода должны выполняться последовательно и, тем самым, не могут быть распараллелены. С другой стороны, выполняемые на каждой итерации алгоритма действия являются независимыми и могут реализовываться одновременно. Так, например, определение ребра наименьшего веса, исходящего из оптимального каркаса в вершину у, которая еще не принадлежит каркасу, может осуществляться для каждой вершины y в отдельности.

Распределение данных между процессорами вычислительной системы должно обеспечивать независимость данной операции алгоритма Прима. В частности, это может быть реализовано, если каждая вершина графа располагается на процессоре вместе со всей связанной с вершиной информацией. Соблюдение данного принципа приводит к тому, что при равномерной загрузке каждый процессор P_j, 1 <= j <= p, где p - количество процессоров, должен содержать:

1. набор вершин
   
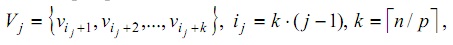
   где n - количество вершин в графе
2. матрицу смежности графа G
   
3. общую часть множества U вершин строящегося дерева

Таким образом, параллельный алгоритм Прима можно представить следующим образом:

U := {a}, где а - произвольная вершина графа
F := "Пустое множество"
W := V - {a}
while W непусто do

1. на каждом процессе найти ребро наименьшего веса e_j=(x, y) среди всех таких ребер, у которых х принадлежит U, а y принадлежит V_j и W
   
2. собрать все e_j на процессе с рангом 0
   
3. на процессе с рангом 0 выбрать ребро e, минимальное из всех e_j
   
4. на процессе с рангом 0 F := F + {e}
   
5. на процессе с рангом 0 U := U + {y}
   
6. на процессе с рангом 0 W := W - {y}
   
7. обновить на всех процессах множество U

Анализ эффективности

Общий анализ сложности параллельного алгоритма Прима даёт идеальные показатели эффективности:

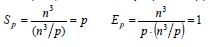
Следует отметить, что в ходе параллельных вычислений идеальная балансировка вычислительной нагрузки процессоров может быть нарушена. В зависимости от вида исходного графа G количество выбранных вершин в охватывающем дереве на разных процессорах может оказаться различным и распределение вычислений между процессорами станет неравномерным (вплоть до отсутствия вычислительной нагрузки на отдельных процессорах). Однако такие предельные ситуации нарушения балансировки в общем случае будут возникать достаточно редко.

Для утчнения полученных показателей эффектиности параллельных вычислений оценим более точно количество вычислительных операций алгоритма и учтем затраты на выполнение операций передачи данных между процессорами.

На каждой итерации параллельного алгоритма Прима происходят операции трех групп:

1. На каждом процессоре - выбор ребра с наименьшим весом w(e_j) со стартовой вершиной, принадлежащей строящемуся каркасу, и финишной вершиной среди имеющихся на процессоре вершин. Принимая за k число вершин в каркасе на момент итерации, можно оценить трудоемкость как

k*(n-k)/p

2. Пересылка номеров ребер с минимальными на данных процессорах весами на главный процессор.

α log₂p + 3ω(p-1)/β ,

где α – латентность сети передачи данных, β – пропускная способность сети, а ω есть размер одного элемента пересылаемых данных в байтах (коэффициент 3 в выражении соответствует числу передаваемых значений между процессорами – длина минимальной дуги и номера 2 вершин, которые соединяются этой дугой).

3. Рассылка на все процессоры с главного обновленного множества вершин каркаса. Трудоемкость оценивается как

log₂p(α + ω/β)

Поскольку за все итерации k меняется от 1 до n-1, то с учетом всех полученных соотношений, общее время выполнения параллельного алгоритма Прима составляет:

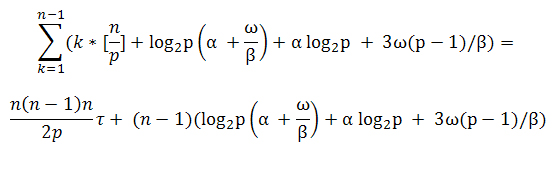
Результаты вычислительных экспериментов

Эксперименты проводились на ПК со следующими характеристиками:

Процессор - Intel Core i5 CPU M 430 2.27 GHz with Hyper Threding
Оперативная память - 4 GB
Операционная система - MS Windows 7 HP x64
Компилятор - MS Visual Studio 2010
α = 0 c
β = 1187600377 байт/c
ω = 4 байта
τ = 2.5 нс

Результаты:

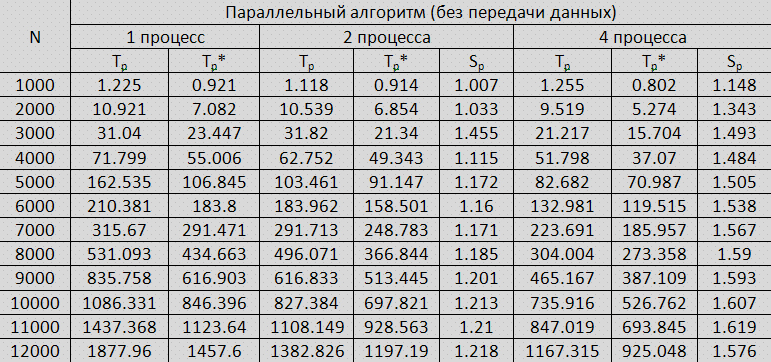
Об авторах

Работу выполнили студенты группы 84-09 факультета ВМК Матвеичев Дмитрий Сергеевич и Хазимов Ян Тагирович.