Введение

Умножение матрицы на вектор широко используется на различных этапах решения прикладных задач. Часто данную операцию необходимо производить множество раз на протяжении всего процесса выполнения задачи, на что тратится большое время. Для оптимизации времени выполнения используются разные алгоритмы умножения, так же применяют специальные библиотеки, решающие эту задачу. Одним из методов оптимизации умножения матрицы на вектор является распределение вычислений на многоядерных системах. В данной работе будет рассмотрен блочный алгоритм параллельного умножения матрицы на вектор.

Последовательный алгоритм

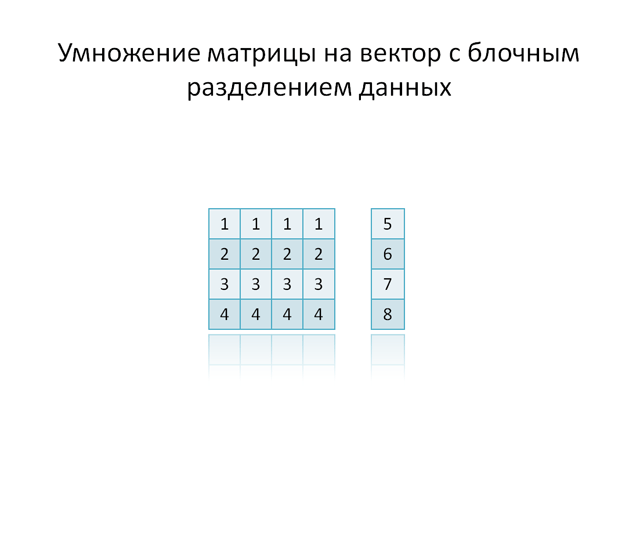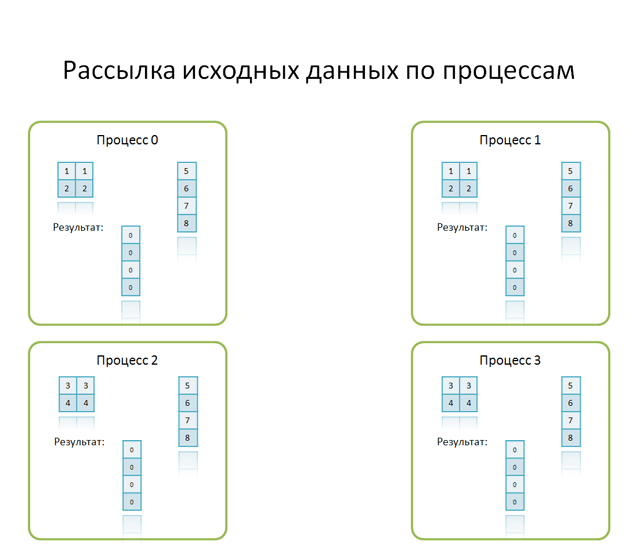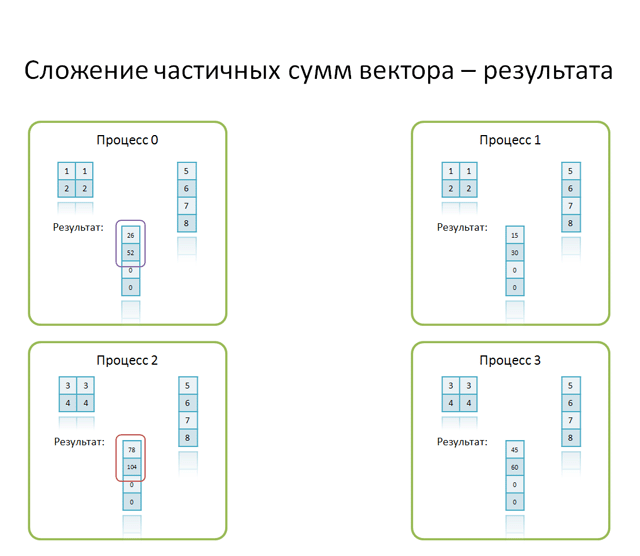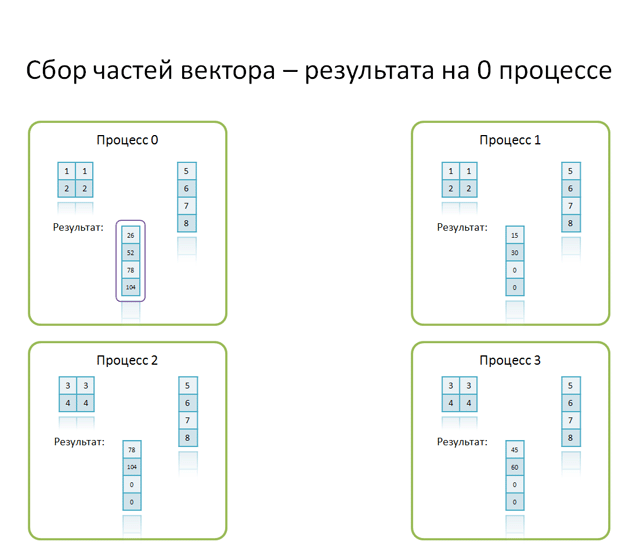
При последовательном умножении матрицы на вектор, скалярно умножается i-я строка матрицы на вектор, результат записывается в i-ю компоненту результирующего вектора.

Параллельный алгоритм с блочным разбиением

При разделении элементов матрицы на блоки, каждому процессу распределяется блок элементов исходной матрицы. В результате скалярного умножения строк блока на соответствующие элементы вектора b, на каждом процессе размещается часть вектора с. Для сбора результирующего вектора необходимо просуммировать частичные результаты, затем собрать все компоненты вектора с в надлежащем порядке.

Оценка сложности

При оценке эффективности принимается несколько предположений: перемножаемая матрица квадратная, операции сложения и умножения выполняются за одинаковое время, вычислительная система однородна. При последовательном умножении матрицы на вектор количество вычислительных операций составляет T=n^2. При параллельном алгоритме количество вычислительных операций составляет T=(n^2)/p. Показатели ускорения и эффективности имеют вид S=(n^2)/(n^2/p)=p E=(n^2)/(p*(n^2/p))=1 Общее время работы алгоритма с блочным разбиением матрицы(решетка имеет вид p=s*q) составляет T=(n/s)(2(n/q)-1)t+(a+w(n/s)/b)log_2(q) где a - латентность вычислительной сети, b - пропускная способность вычислительной сети, w - размер одного элемента в байтах, t - время выполнения одной арифметической операции(предположим что умножение и сложение выполняется за одно время).

Демонстрация работы алгоритма

Серийные тесты

Эксперименты проводились на двухпроцессорном вычислителе на базе двухядерных процессоров Intel Core 2 Duo, 2.33 Ггц, 4 Гб RAM, Microsoft Windows 7 Enterprise 2010. Связь между узлами 1 Gigabit Ethernet. IDE Microsoft Visual Studio 2008, стандартный компилятор, Microsoft MPI. Параметры теоретических зависимостей в данной вычислительной системе имеют значения: t - 2.25 нсек, латентность - 44мсек, пропускная способность - 39,73 Мбайт/с и величина w равна 8 байт.

Размер матрицы	Последоваетльный алгоритм / Параллельный алгоритм в один процесс, с	Параллельный алгоритм
		4 процесса			9 процессов
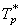
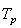
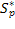
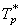
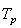
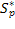
1200	0,0022/0,0126	0,1621	0,0061	0,0135	0,7250	0,0052	0,0030
2400	0,0087/0,0485	0,7173	0,0111	0,0121	1,1002	0,0075	0,0079
3600	0,0195/0,1082	1,6934	0,0193	0,0115	1,6064	0,0112	0,0121
4800	0,0346/0,1992	3,6657	0,0307	0,0094	2,8770	0,0164	0,0120
6000	0,0541/0,2992	7,6920	0,0454	0,0070	5,5284	0,0230	0,0097

Вывод

По результатам серийных экспериментов можно увидеть, что результаты реальных вычислений отличаются от теоретических оценок. Это связанно с тем, что параллельные алгоритмы имеют накладные расходы в виде пересылок данных между процессами. Из этого можно сделать вывод, что эффективность параллельного алгоритма будет тем ближе к теоретической чем меньше будет пересылок данных между процессами.

Список литературы

1. Гергель В.П. Теория и практика параллельных вычислений. // Интуит Бином. Лаборатория знаний. 2007. - 424 с.
2. Антонов, Шпаковский, Серикова, Корнеев. Сборник MPI. 2009