Постановка задачи и используемые подходы

Рассматривается конечномерная задача оптимизации (задача нелинейного программирования)


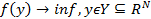
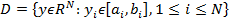
т.е. задача отыскания экстремальных значений целевой (минимизируемой) функции f (y) в области Y , задаваемой координатными ограничениями [1,4].

Не уменьшая общности, далее будем считать, что поставлена задача нахождения минимума. Одним из подходов к решению многомерной задачи оптимизации является сведение многомерной задачи к одномерной. Это может быть сделано разными способами. Наиболее эффективными являются многошаговая схема оптимизации и редукция размерности на основе кривых Пеано, о которой далее и пойдет речь. Данная схема основана на известном фундаментальном факте, согласно которому N -мерный гиперпараллелепипед и отрезок [0, 1] вещественной оси являются равномощными множествами, и отрезок [0,1] может быть однозначно и непрерывно отображен на гиперпараллелепипед. Такие отображения и называются кривыми (или развертками) Пеано [1, 2]. На рис. 1 изображен образ отрезка [0,1] при отображении пеаноподобной разверткой при разбиении третьего порядка.

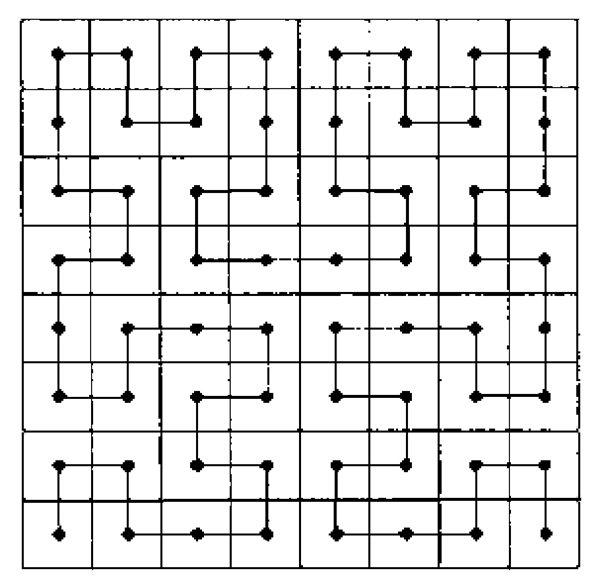
Рисунок 1. Образ отрезка [0,1] при отображении пеаноподобной разверткой третьего порядка

В качестве основного алгоритма решения была выбрана модификация информационно-статистического алгоритма глобального поиска (АГП) – многомерный обобщенный алгоритм глобального поиска (МОАГП), который состоит в следующем:

1. Измеряем значения функции на концах отрезка, полагаем k=2
2. Для каждого интервала:
• Вычисляем характеристику интервалапо следующему правилу:
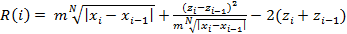  , где
  
  
  
  
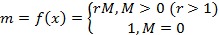
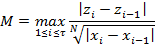
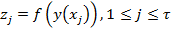
3. На подинтервале с максимальной характеристикой ставим новую точку по правилу:
   
   
   

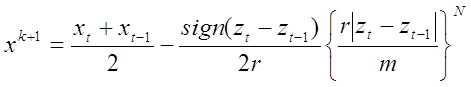
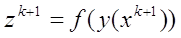
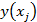- точка N - мерного гиперпараллелепипеда, являющаяся образом точке 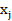отрезка [0,1].

В качестве алгоритма для сравнения используется метод перебора, который разбивает отрезок на заданное количество частей и ищет минимум среди значений функций в этих точках.

Искомый глобальный минимум будем искать согласно следующему алгоритму:

1. Запускаем К потоков, пронумерованных 0, 1, …, К-1 соответственно.
2. Отрезок [0,1] также разбиваем на K отрезков, пронумерованных 0, 1, …, К-1.
3. Потоку i соответствует отрезок с тем же номером. Каждый поток ищет минимум на своем отрезке. Важно, что потоки не обмениваются информацией относительно найденных точек, т.о. каждый поток находит свой минимум на своем участке. Данные о найденных минимумах передаются потоку с номером 0.
4. Находим минимальное из тех значений, что найдены в каждом потоке. Эта часть является последовательно исполняемой.

Следует отметить, что потоки не получают никакой дополнительной информации о результатах поиска минимума на каждом из них.

Параметр надежности алгоритма выбран равным 2,4. Это значение было выбрано экспериментально, поскольку при нем удается получить решение всех задач тестового набора при относительно небольшом числе испытаний. Важным параметром параллельной реализации алгоритма является число K начальных отрезков, на которые разбивается исходный отрезок. Следует напомнить, что в каждой подобласти независимо от других запускается параллельный поток, в котором выполняется алгоритм поиска глобального минимума. В каждом потоке разрешается выполнить по М испытаний. Тем самым общее число выполненных испытаний составит К∙М.

Эксперименты с одной разверткой на всей области

В наших численных экспериментах было использован класс тестовых функций, порожденных GKLS-генератором [3]. Этот генератор обладает несколькими преимуществами, которые позволяют использовать его в качестве хорошего инструмента для сравнения численных алгоритмов.

Он генерирует классы 100 тестовых функций с одинаковым числом локальных минимумов и предоставляет полную информацию о каждой функции: ее размерность, значения всех локальных минимумов, их координаты, области притяжения, и т.д. Существует возможность с легкостью генерировать более сложные или более простые тестовые классы. Только 5 параметров должны быть определены пользователем, а остальные генерируются случайным образом. Важная особенность генератора состоит в полной повторяемости экспериментов: если вы используете те же самые 5 параметров, то при каждом запуске генератор будет порождать такой же класс функций [3].

На следующих графиках представлены результаты испытаний, зависимости времени и надежности от количества разбиений отрезка:

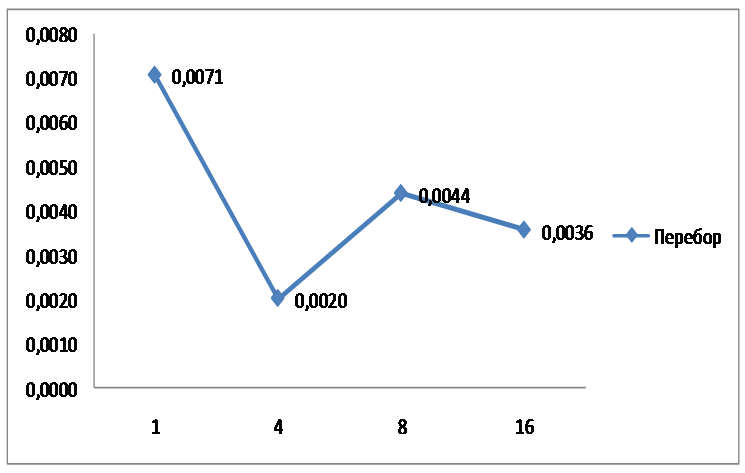
Рис. 1. Время работы алгоритма перебора на 1, 4, 8, 16 потоках при делении отрезка на 8000 частей.


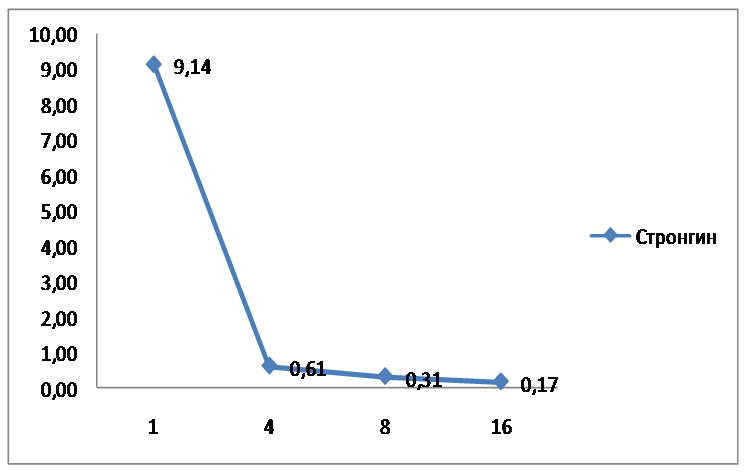
Рис. 2. Время работы алгоритма Стронгина на 1, 4, 8, 16 потоках при делении отрезка на 8000 частей.


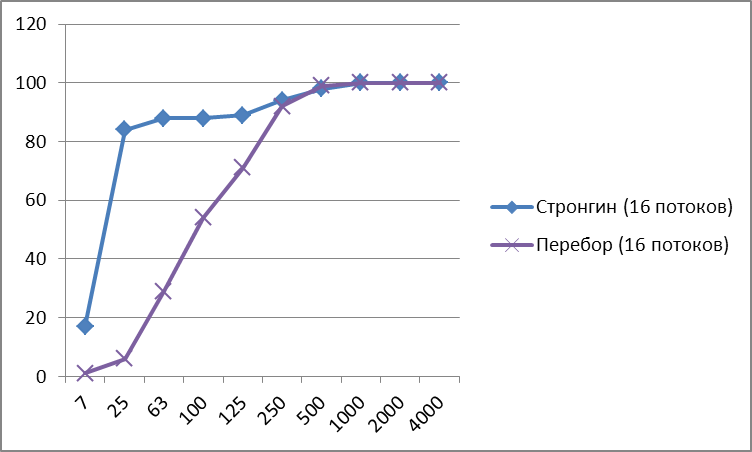
Рис. 3. Сравнение степени надежности алгоритмов перебора и Стронгина.

При проведении исследований дополнительно были выполнены оценки ускорения непосредственно по времени (рис. 1 и 2). При этом замерялось среднее время до момента определения с заданной точностью глобально-оптимального решения (или до исчерпания установленного максимального числа итераций, если решение не определялось). Усреднение проводилось по всем 100 функциям GKLS-генератора. Испытания проводились на процессоре Intel Quad 6600 2.4 GHz, 2 Gb RAM, 32 bit OS. В данной реализации в качестве основного инструмента выбрана технология MPI.

По результатам испытаний видно, что параллельная реализация сильно выигрывает перед последовательной.

Заключение

Как видно из результатов, использование параллельных вычислений в который раз доказало свою эффективность. Как видно ускорение по времени с ростом числа потоков неуклонно растет. Приведенные результаты показывают, что использование параллельных вычислений в данной области оправдано.

Однако же использование МОАГП на большом количестве потоков может оказаться нецелесообразным, т.к. реализация равномерного перебора с аналогичным способом распараллеливания дает отличный результат на малых размерностях. Фактически, данная реализация МОАГП вырождается в равномерный перебор.

Литература

1. Городецкий С.Ю., Гришагин В.А. Учебный курс «Модели и методы конечномерной оптимизации». Часть 2 «Нелинейное программирование и многоэкстремальная оптимизация». Нижний Новгород , 2003.
2. Lera D., Sergeyev Ya.D. (2010) Lipschitz and Holder global optimization using space-filling curves, Applied Numerical Mathematics, 60(1-2), 115–129.
3. M. Gaviano, D.E. Kvasov, D. Lera, Ya.D. Sergeyev, Software for generation of classes of test functions with known local and global minima for global optimization, ACM TOMS 29 (4) (2003) 469–480.
4. В.А. Гришагин. Параллельные алгоритмы многоэкстремальной оптимизации в областях с вычислимой границей. Высокопроизводительные параллельные вычисления на кластерных системах, 2007.

Авторы

Лабораторную работу выполнили студенты группы 8409 факультета ВМК: Кукаева Светлана, Грачев Андрей