Постановка задачи
Систему линейных уравнений можно записать в виде Ах=b, где А - вещественная матрица размера n на n, b - вектор размера n, х - вектор неизвестных размера n . Соответственно решение системы линейных уравнений - это нахождение вектора x, при подстановке которого в
систему все её уравнения обращаются в верные равенства. Общий вид системы линейных уравнений приведён в (1).

Существует немало методов для практического нахождения решений систем линейных уравнений. Одним из самых известных является метод Гаусса. Решение системы линейных уравнений при помощи метода Гаусса основывается на том, что от заданной системы, переходят к эквивалентной, которая решается проще, чем исходная.
В работе требуется
- Реализовать последовательную и параллельную при вертикальным разбиением матрицы по столбцам(с
использованием библиотеки MPI) версии метода Гаусса для решения систем линейных уравнений;
- Получить оценки вычислительной сложности для последовательной и параллельной версий алгоритма;
- Провести эксперименты на одних и тех же данных при разном количестве процессов, проанализировать полученные результаты.
Метод решения
Метод Гаусса состоит из двух этапов. Первый этап - это прямой ход, в результате которого расширенная матрица системы путём элементарных преобразований (перестановка уравнений системы, умножение уравнений на число, отличное от нуля, и сложение уравнений) приводится к верхнетреугольному виду. На втором этапе (обратный ход) происходит вычисление значений неизвестных.
Прямой ход метода Гаусса состоит в последовательном исключении неизвестных в уравнениях решаемой системы. Строка, которая используется для исключения неизвестных, называется ведущей. На i итерации (где i
изменяется от 0 до n) производится исключение i неизвестной из всех строк, не бывших ведущими на
предыдущих итерациях. Для этого из этих уравнений вычитается ведущая строка,
домноженная на (a[k,i]/a[i,i]) для того, чтобы результирующие коэффициенты в этих строках при i неизвестной занулились.
Обратный ход последовательно проходит по всем строкам в
порядке убывания номера итерации, на которой они были ведущими. Для каждой такой
строки производится вычисление соответствующей переменной по следующим
формулам:

Параллельная схема
Для реализации параллельного метода Гаусса в данной работе используется вертикальное разбиение матрицы по столбцам. Для этого столбцы исходной матрицы распределяются между процессами.
При прямом ходе на каждой итерации выбирается один из
процессов, который осуществляет выбор ведущего элемента среди своей части
матрицы (максимального по модулю отличного от нуля и находящегося на строке, которая ещё не использовалась в качестве ведущей). В случае если такой элемент обнаружен, то этот процесс осуществляет подсчёт коэффициентов, на которые необходимо домножить элементы ведущей строки при её вычитании из других строк и рассылает этот массив всем остальным процессам. Для элементов, расположенных в строках, которые были ведущими на предыдущих итерациях, коэффициенты устанавливаются равными нулю. Далее все процессы выполняют обработку своих частей матрицы по столбцам. Для каждого своего столбца они находят элемент, находящийся на ведущей строке и вычитают его из остальных элементов, расположенных на других строках в данном столбце, домножив на соответствующий коэффициент. Нулевой процесс осуществляет обработку вектора. Затем выбирается другой процесс и действия повторяются.
Перед выполнением обратного хода элементы массива для хранения вектора
результата зануляются, а нулевой процесс рассылает всем
остальным обработанный при прямом ходе вектор. При выполнении обратного хода ищется элемент, который был
ведущим на i итерации (i изменяется от n-1 до
0), номер его строки и столбца, а также номер процесса, осуществившего эту
итерацию. На каждой итерации все процессы суммируют коэффициенты своих
частей обрабатываемой матрицы, находящиеся на ведущей строке, умножив их на
соответствующее столбцу, где находится данный элемент, значение
неизвестной. Затем они посылают ведущему процессу полученные результаты.
Ведущий процесс вычисляет значение соответствующей выбранному столбцу
неизвестной и рассылает его всем остальным процессам. Далее действия повторяются
при уменьшении i на единицу.
Анализ эффективности
Пусть n это порядок решаемой системы линейных
уравнений, а р -число используемых процессоров.
Общее время выполнения последовательного варианта метода Гаусса
составляет
При выполнении прямого хода алгоритма на каждой итерации для выбора ведущей
строки каждый процессор должен осуществить выбор максимального значения в
столбце с исключаемой неизвестной в пределах своей полосы.
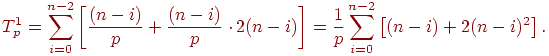
С учетом
выполняемого количества итераций общее число операций параллельного варианта
прямого хода метода Гаусса определяется выражением:

На каждой итерации обратного хода метода Гаусса после
рассылки вычисленного значения очередной неизвестной каждый процессор должен
обновить значения правых частей для всех строк, расположенных на этом
процессоре. Отсюда следует, что трудоемкость параллельного варианта обратного
хода метода Гаусса оценивается как величина:

Просуммировав полученные выражения, получим

Как результат выполненного анализа, показатели
ускорения и эффективности параллельного варианта метода Гаусса могут быть
определены при помощи соотношений следующего вида:

Также при выполнении прямого хода на каждой итерации выполняется рассылка
массива коэффициентов. Сложность такой операции получается равной
Т[p,1](comm)=(n-1)logp(a+wn/b).
Кроме этого, на каждой итерации всем процессам
рассылаются данные с номерами ведущих строки и столбца, а также номер ведущего
процесса, что можно оценить
Т[p,2](comm)=(n-1)logp(a+w/b).
При выполнении обратного хода алгоритма Гаусса на каждой
итерации осуществляется рассылка вычисленных неизвестных, что оценивается
Т[p,3](comm)=(n-1)logp(a+wn/b).
Кроме этого, на каждой итерации осуществляется сборка
значений со всех процессов с суммированием, что можно оценить как
Т[p,4](comm)=(n-1)logp(a+w/b).
Результаты вычислительных
экспериментов
Тестирование последовательной и параллельной версий проводилось на компьютере со следующими характеристиками:
Intel Core 2 Duo CPU T5550 1,83ГГц, 3.00 ГБ
ОЗУ под управлением OS Microsoft Windows XP Professional sp3, латентность -
0,000015 с, пропускная способность - 47 Мбайт/с.
|
Размер матрицы |
Последовательный алгоритм/Параллельный, запущенный на 1 процессе |
2 процесса |
4 процесса |
|
T* |
T |
S* |
T* |
T |
S* |
|
500 |
0,2195/4,0701 |
1,8612 |
1,4011 |
0,1179 |
1,6592 |
0,821 |
0,1322 |
|
1000 |
2,5937/34,7503 |
17,7041 |
10,3812 |
0,1465 |
17,6353 |
6,3248 |
0,147 |
|
1500 |
8,7587/118,1184 |
58,9231 |
34,9893 |
0,1486 |
59,1328 |
17,5657 |
0,1481 |
|
2000 |
20,5978/280,4308 |
143,7514 |
83,7235 |
0,1432 |
143,1692 |
48,7488 |
0,1438
|
|
2500 |
40,0948/543,7459 |
270,6686 |
163,5698 |
0,1481 |
263,6951 |
89,9438 |
0,152 |
T - теоритическая оценка времени выполнения алгоритма, Т* - время выполнения
алгоритма на практике, S* - ускорение, по данным экспериментов.
Об авторе
Выполнила Сергеева Екатерина группа
8303



