Постановка задачи

Необходимо выполнить реализацию параллельного алгоритма сортировки пузырьком.

Необходимо провести вычислительные эксперименты.

Необходимо построить теоретические оценки с учетом параметров используемой вычислительной системы.

Сравнить полученные оценки с экспериментальными данными.

Метод решения

Сортировка является одной из типовых проблем обработки данных и обычно понимается как задача размещения элементов неупорядоченного набора значений S={a1,a2,a3,..,an} в порядке монотонного возрастания или убывания S~S’={{a1’,a2’,…an’}: a1’<=a2’<=…<=an’} Алгоритм сортировки пузырьком сравнивает и обменивает соседние элементы в последовательности, которую нужно отсортировать. Для последовательности (a1,a2,a3,..,an) алгоритм сначала выполняет n-1 базовых операций "сравнения-обмена" для последовательных пар элементов (a1, a2), (a2, a3), ..., (an-1,an). В результате после первой итерации алгоритма самый большой элемент перемещается ("всплывает") в конец последовательности. Далее последний элемент в преобразованной последовательности может быть исключен из рассмотрения, и описанная выше процедура применяется к оставшейся части последовательности (a'1, a'2, ..., a'n-1).
Алгоритм сортировки

BubbleSort(double A[], int n)
{
for(i = 1; i < n; i++)
for(j = 0; j < n - i; j++)
compare_exchange(A[j], A[j+1]);

}

Параллельная схема

Алгоритм пузырьковой сортировки в прямом виде достаточно сложен для распараллеливания – сравнение пар значений упорядочиваемого набора данных происходит строго последовательно. В связи с этим для параллельного применения используется не сам этот алгоритм, а его модификация, известная в литературе как метод чет-нечетной перестановки (odd-even transposition). Суть модификации состоит в том, что в алгоритм сортировки
вводятся два разных правила выполнения итераций метода – в зависимости от четности или нечетности номера итерации сортировки для
обработки выбираются элементы с четными или нечетными индексами соответственно, сравнение выделяемых значений всегда осуществляется
с их правыми соседними элементами. Таким образом, на всех нечетных итерациях сравниваются пары (a1, a2), (a3, a4), ..., (an-1, an) (при четном n), а на четных итерациях обрабатываются элементы (a2, a3), (a4, a5), ..., (an-2,an-1). После n- кратного повторения итераций сортировки исходный набор данных оказывается упорядоченным.
Алгоритм параллельной сортировки

ParallelOddEvenSort(double A[], int n)
{
int id = GetProcId();
int n= GetProcNum();
for (int i=0; i{
if ( i%2 == 1 )
{
if ( id%2 == 1 )
{
if ( id < n-1 ) compare_split_min(id+1);

}
else
if ( id > 0 ) compare_ split_max(id-1);
}

if ( i%2 == 0 )
{
if( id%2 == 0 )
{
if ( id < n-1 ) compare_ split_min(id+1);

}
else
compare_ split_max(id-1);
}
}
}

Анализ Эффективности

На начальной стадии работы метода каждый процессор проводит упорядочивание своих блоков данных (размер блоков при равномерном распределении данных равен n/p). Предположим, что данная начальная сортировка может быть выполнена при помощи быстродействующих алгоритмов упорядочивания данных, тогда трудоемкость начальной стадии вычислений можно определить выражением вида:
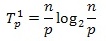
Далее, на каждой выполняемой итерации параллельной сортировки взаимодействующие пары процессоров осуществляют передачу блоков между собой, после чего они объединяются при помощи процедуры слияния. Общее количество итераций не превышает величины p, и, как результат, общее количество операций этой части параллельных вычислений оказывается равным:
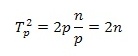
С учетом полученных соотношений показатели эффективности и ускорения параллельного метода сортировки имеют вид:
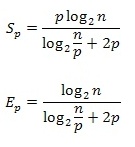
Учитывая длительность выполняемых вычислительных операций и оценивая трудоемкость операции передачи блоков между процессорами, общее время всех выполняемых в ходе сортировки операций передачи блоков оценивается так:
где α– латентность, β – пропускная способность сети передачи данных, а ω есть размер элемента упорядочиваемых данных в байтах.
Общее время выполнения параллельного алгоритма сортировки:

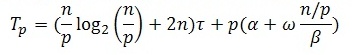
где τ есть время выполнения базовой операции сортировки.

Результаты вычислительных экспериментов

Тестовая инфраструктура

Процессор - Intel Core 2 Duo E6550 2.33 GHz
Оперативная память - 4 GB
Операционная система - MS Windows 7 x64
Компилятор - MS Visual Studio 2008
Скорость обмена между процессами ~ 7 Gbit/s
Время выполнения базовой операции перестановки ~ 10 ns
Размер элемента набора - 8 byte (double)




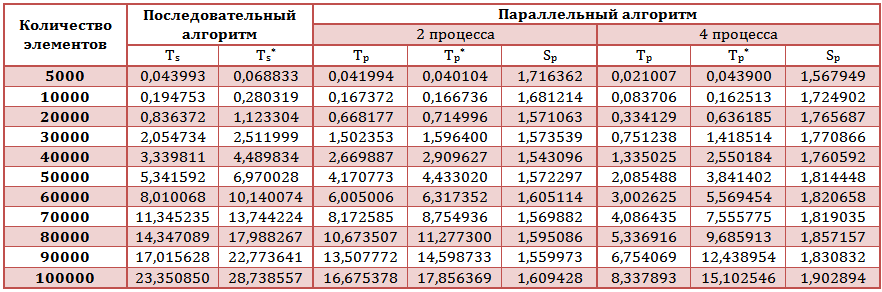
где
Tw - теоретическое время выполнения алгоритма(w=s - последовательного,w=p - параллельного),
Tw* - практическое(w=s - последовательного,w=p - параллельного),
Sp - практическое ускорение

Об авторе

Работу выполнила студентка группы 8409 Добролюбова О.В.