Постановка задачи
Сортировка-это одна из типовых проблем обработки данных.Под сортировкой понимается размещение элементов неупорядоченного набора значений в порядке монотонного возрастания или убывания.Вычислительная трудоемкость процедуры упорядочивания является достаточно высокой. Так, для сортировки пузырьком количество необходимых операций определяется квадратичной зависимостью от числа упорядочиваемых данных
Ускорение сортировки может быть обеспечено при использовании нескольких (p>1) процессоров. Исходный упорядочиваемый набор в этом случае разделяется между процессорами; в ходе сортировки данные пересылаются между процессорами и сравниваются между собой.
В ходе лабораторной работы требуется реализовать параллельный алгоритм сортировки пузырьком,а так же сравнить время выполнения последовательного и параллельного алгоритмов.
Описание метода
Последовательный алгоритм:
Последовательный алгоритм пузырьковой сортировки сравнивает и обменивает соседние элементы в последовательности, которую нужно отсортировать. Для последовательности
(a1, a2,…, an)
алгоритм сначала n-1 раз выполняет операции сравнения и обмена между элементами последовательных пар:
(a1, a2), (a2, a3), ..., (an-1,an).
После завершения итерации самый большой элемент последовательности перемещается («всплывает») в её конец. Далее алгоритм повторяется для последовательности
(a'1, a'2, ..., a'n-1).
Где последний элемент исключён из рассмотрения. Последовательность будет отсортирована после n-1 итерации.
Этот алгоритм в прямом виде достаточно сложен для распараллеливания (сравнение пар значений упорядочиваемого набора данных происходит строго последовательно)поэтому в параллельной версии программы используется не сам этот алгоритм, а его модификация, а именно алгоритм чет-нечетной перестановки:
Алгоритм чет-нечетной перестановки:
В алгоритм сортировки вводятся два разных правила выполнения итераций метода: в зависимости от четности или нечетности номера итерации сортировки для обработки выбираются элементы с четными или нечетными индексами соответственно, сравнение выделяемых значений всегда осуществляется с их правыми соседними элементами. Таким образом, на всех нечетных итерациях сравниваются пары
(a1, a2), (a3, a4), ..., (an-1,an) (при четном n),
а на четных итерациях обрабатываются элементы (a2, a3), (a4, a5), ..., (an-2,an-1).
После n-кратного повторения итераций сортировки исходный набор данных будет упорядоченным.
Описание параллельной схемы
Сначала главный процессор разбивает исходный массив на p равных частей, где n кол-во процессов, каждый блок содержит n/p элементов массива. Полученные блоки рассылаются по процессам. Далее идет предобработка. На этапе предобработки каждый процесс сортирует свой массив методом последовательной сортировки. Далее происходит чередование чет-нечетных перестановок на p итерациях. На нечетной итерации пары процессов с номерами (0,1)(2,3)(4,5)… обмениваются друг с другом массивами, после чего на процессе с меньшим номером остается n/p первых упорядоченных элементов объединенного массива, а на процессе с большим номером остается n/p последних упорядоченных элементов объединенного массива. На четной итерации происходит все точно так же, но обмен производится между процессами с номерами (1,2)(3,4)(5,6)(7,8)… . Если в течении 2-х последовательных четной и нечетной итерации не производится никаких изменений, то алгоритм может прекратить свою работу заранее. После этого части массивов отсылаются на главный процесс и там объединяются, после чего получается отсортированный массив.
Реализация::
#include "stdio.h"
#include "mpi.h"
#include "fstream"
double startT, stopT;
int* mergeArrays (int* v1, int n1, int* v2, int n2)
{
int i, j, k;
int* result;
result = new int[n1 + n2];
i = 0;
j = 0;
k = 0;
while (i < n1 && j < n2)
if (v1[i] < v2[j]) {
result[k] = v1[i];
i++;
k++;
} else {
result[k] = v2[j];
j++;
k++;
}
if (i == n1)
while (j < n2) {
result[k] = v2[j];
j++;
k++;
}
if(j == n2)
while (i < n1) {
result[k] = v1[i];
i++;
k++;
}
return result;
}
void swap (int* v, int i, int j)
{
int t;
t = v[i];
v[i] = v[j];
v[j] = t;
}
void sort (int* v, int n)
{
int i, j;
for (i = n - 2; i >= 0; i--)
for (j = 0; j <= i; j++)
if (v[j] > v[j + 1])
swap (v, j, j + 1);
}
using namespace std;
void main (int argc, char ** argv)
{
int* data; //Our unsorted array
int* resultant_array; //Sorted Array
int* sub;
int m, n;
int id, p;
int r;
int s;
int i;
int z;
int move;
MPI_Status status;
MPI_Init (&argc, &argv);
MPI_Comm_rank (MPI_COMM_WORLD, &id);
MPI_Comm_size (MPI_COMM_WORLD, &p);
//Task Of The Master Processor
if (id == 0) {
n = 80000;
s = n / p;
r = n % p;
data = new int[n + s - r];
srand(unsigned int(MPI_Wtime()));
ofstream file("input");
for(i = 0; i < n; i++)
{
data[i] = rand() % 15000;
file << data[i] << " ";
}
file.close();
if (r != 0) {
for (i = n; i < n + s - r; i++)
data[i] = 0;
s = s + 1;
}
startT = MPI_Wtime(); //Start The Time.
MPI_Bcast (&s, 1, MPI_INT, 0, MPI_COMM_WORLD);
resultant_array = new int[s]; //Allocating result array
//Sending data array from master to all other slaves
MPI_Scatter (data, s, MPI_INT, resultant_array, s, MPI_INT, 0, MPI_COMM_WORLD);
sort (resultant_array, s);
} else {
MPI_Bcast (&s, 1, MPI_INT, 0, MPI_COMM_WORLD);
//Allocating resultant array
resultant_array = new int[s];
MPI_Scatter (data, s, MPI_INT, resultant_array, s, MPI_INT, 0, MPI_COMM_WORLD);
//Each slave processor will sort according to the array partitioning n/p
sort (resultant_array, s); //Sort the array up to index s.
}
move = 1;
//Merging the sub sorted arrays to obtain resultant sorted array
while (move < p) {
if (id%(2*move)==0) {
if (id + move < p) { //Receive
MPI_Recv (&m, 1, MPI_INT, id + move, 0, MPI_COMM_WORLD, &status);
sub = new int [m]; //Allocate space for sub array
MPI_Recv (sub, m, MPI_INT, id + move, 0, MPI_COMM_WORLD, &status);
//Obtaing resultant array by merging sub sorted array
resultant_array = mergeArrays (resultant_array, s, sub, m);
s = s + m;
}
} else { //Send datas to neighbour processors
int near = id - move;
MPI_Send (&s, 1, MPI_INT, near, 0, MPI_COMM_WORLD);
MPI_Send (resultant_array, s, MPI_INT, near, 0, MPI_COMM_WORLD);
break;
}
move = move * 2;
}
//Final Part, In this part Master CPU outputs the results.!!!
if (id == 0) {
stopT = MPI_Wtime();
double parallelTime = stopT- startT;
printf("\n\n\nTime: %f", parallelTime);
startT = MPI_Wtime();
sort(data,n);
stopT = MPI_Wtime();
double poslTime = stopT - startT;
printf("\n Time: %f", stopT - startT);
printf("\n SpeedUp: %f \n\n\n", poslTime/parallelTime);
ofstream file("output");
for(i = 0; i < n; i++)
{
file << resultant_array[i] << " ";
}
file.close();
}
MPI_Finalize (); //Finalize MPI environment.
}
Анализ эффективности
На начальной стадии работы метода каждый процессор проводит упорядочивание своих блоков данных (размер блоков при равномерном распределении данных равен n/p). Предположим, что данная начальная сортировка может быть выполнена при помощи быстродействующих алгоритмов упорядочивания данных, тогда трудоемкость начальной стадии вычислений можно определить выражением вида:
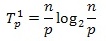
Далее, на каждой выполняемой итерации параллельной сортировки взаимодействующие пары процессоров осуществляют передачу блоков между собой, после чего получаемые на каждом процессоре пары блоков объединяются при помощи процедуры слияния. Общее количество итераций не превышает величины p, и, как результат, общее количество операций этой части параллельных вычислений оказывается равным:
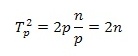
С учетом полученных соотношений показатели эффективности и ускорения параллельного метода сортировки имеют вид:
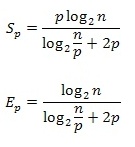
Результаты экспериментов

CPU: Intel(R) Core(TM) 2 Quad CPU Q6850 @ 2.33GHz
RAM : 4096 MB DDR2
Cores: 4
L1 D-Cache: 32 KBytes x4
L1 I-Cache: 32 KBytes x4
L2 Cache: 4096 KBytes x4
Демонстрация
Об авторе
Работу выполнила студентка группы 83-03 факультета ВМК Гурьянова Ольга |



