Постановка задачи
Результатом перемножения матриц А и B является матрица С, каждый элемент которой есть скалярное произведение соответствующих строк матрицы A и столбцов матрицы B.
Задача состоит в получении результата перемножения двух случайно заданных квадратных матриц.
Для решения используются последовательный и параллельный алгоритмы, результаты которых нужно сравнить. Параллельный алгоритм разрабатывается на основе последовательного, с целью ускорения выполнения процесса умножения матриц больших размеров. Существует несколько методов распараллеливания алгоритма перемножения матриц. В этой работе будет реализован так называемый ленточный алгоритм.
Последовательный алгоритм
Последовательный алгоритм представляется тремя вложенными циклами и ориентирован на последовательное вычисление строк результирующей матрицы С.
void MatrixMultiplication(double *&A, double *&B, double *&C, int &Size) {
int i, j, k;
Flip(B, Size);
for (i=0; i < Size; i++) {
for (j=0; j < Size; j++) {
C[i*Size+j] = 0;
for (k=0; k < Size; k++)
C[i*Size+j] += A[i*Size+k]*B[j*Size+k];
}
}
}
Этот алгоритм является итеративным и ориентирован на последовательное вычисление строк матрицы С. Предполагается выполнение n•n•n операций умножения и столько же операций сложения элементов исходных матриц. Количество выполненных операций имеет порядок O(n3).
Поскольку каждый элемент результирующей матрицы есть скалярное произведение строки и столбца исходных матриц, то для вычисления всех элементов матрицы С размером n*n необходимо выполнить (n2)*(2n-1) скалярных операций и затратить время T1 = (n2)*(2n-1)*t, где t есть время выполнения одной элементарной скалярной операции.
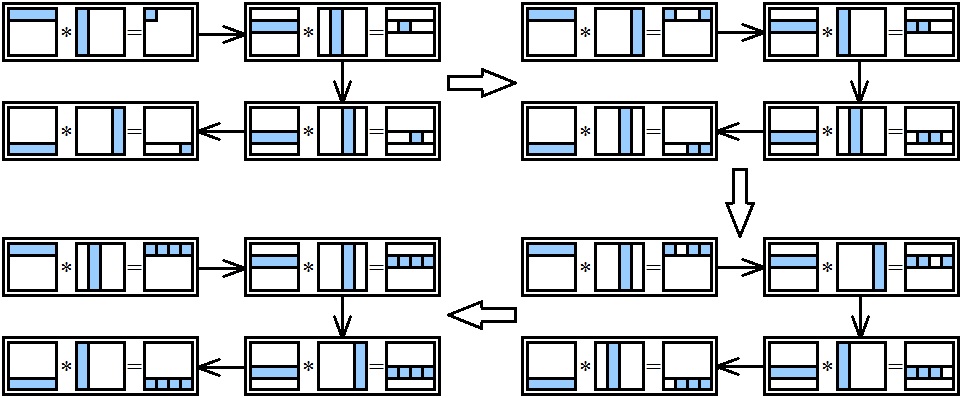
Параллельная схема
Алгоритм представляет собой итерационную процедуру, количество итераций которой совпадает с числом подзадач.
- На каждой итерации алгоритма каждая подзадача содержит по одинаковому количеству строк матрицы А и матрицы В.
- При выполнении итерации проводится скалярное умножение содержащихся в подзадачах строк, что приводит к получению соответствующих элементов результирующей матрицы С.
- По завершении вычислений в конце каждой итерации столбцы матрицы В должны быть переданы между подзадачами с тем, чтобы в каждой подзадаче оказались новые столбцы матрицы В и могли быть вычислены новые элементы матрицы C.
- По завершении итераций строки собираются в единую матрицу C.
При этом данная передача столбцов между подзадачами должна быть организована таким образом, чтобы после завершения итераций алгоритма в каждой подзадаче последовательно оказались все столбцы матрицы В.
Выделенные базовые подзадачи характеризуются одинаковой вычислительной трудоемкостью и равным объемом передаваемых данных. Когда размер матриц n оказывается больше, чем число процессоров p, базовые подзадачи можно укрупнить, объединив в рамках одной подзадачи несколько соседних строк и столбцов перемножаемых матриц. В этом случае исходная матрица A разбивается на ряд горизонтальных полос, а матрица B представляется в виде набора вертикальных полос. Размер полос при этом следует выбрать равным k=n/p (в предположении, что n кратно p), что позволит по-прежнему обеспечить равномерность распределения вычислительной нагрузки по процессорам, составляющим многопроцессорную вычислительную систему.
void MatrixMultiplicationMPI(double *&A, double *&B, double *&C, int &Size) {
int dim = Size;
int i, j, k, p, ind;
double temp;
MPI_Status Status;
int ProcPartSize = dim/ProcNum;
int ProcPartElem = ProcPartSize*dim;
double* bufA = new double[ProcPartElem];
double* bufB = new double[ProcPartElem];
double* bufC = new double[ProcPartElem];
int ProcPart = dim/ProcNum, part = ProcPart*dim;
if (ProcRank == 0) {
Flip(B, Size);
}
MPI_Scatter(A, part, MPI_DOUBLE, bufA, part, MPI_DOUBLE, 0, MPI_COMM_WORLD);
MPI_Scatter(B, part, MPI_DOUBLE, bufB, part, MPI_DOUBLE, 0, MPI_COMM_WORLD);
temp = 0.0;
for (i=0; i < ProcPartSize; i++) {
for (j=0; j < ProcPartSize; j++) {
for (k=0; k < dim; k++)
temp += bufA[i*dim+k]*bufB[j*dim+k];
bufC[i*dim+j+ProcPartSize*ProcRank] = temp;
temp = 0.0;
}
}
int NextProc; int PrevProc;
for (p=1; p < ProcNum; p++) {
NextProc = ProcRank+1;
if (ProcRank == ProcNum-1)
NextProc = 0;
PrevProc = ProcRank-1;
if (ProcRank == 0)
PrevProc = ProcNum-1;
MPI_Sendrecv_replace(bufB, part, MPI_DOUBLE, NextProc, 0, PrevProc, 0, MPI_COMM_WORLD, &Status);
temp = 0.0;
for (i=0; i < ProcPartSize; i++) {
for (j=0; j < ProcPartSize; j++) {
for (k=0; k < dim; k++) {
temp += bufA[i*dim+k]*bufB[j*dim+k];
}
if (ProcRank-p >= 0 )
ind = ProcRank-p;
else ind = (ProcNum-p+ProcRank);
bufC[i*dim+j+ind*ProcPartSize] = temp;
temp = 0.0;
}
}
}
MPI_Gather(bufC, ProcPartElem, MPI_DOUBLE, C, ProcPartElem, MPI_DOUBLE, 0, MPI_COMM_WORLD);
delete []bufA;
delete []bufB;
delete []bufC;
}
Анализ эффективности
Примем за Ts - время работы последовательного алгоритма, за Tp - время работы параллельного алгоритма, за S - ускорение, за E - эффективность, за p – количество процессоров.
При применении последовательного алгоритма перемножения матриц число шагов имеет порядок O(n3).
Для параллельного алгоритма на каждой итерации каждый процессор выполняет умножение имеющихся на процессоре полос исходных матриц А и В (размерность каждой полосы составляет n/p, следовательно, общее количество выполняемых при этом умножении операций равно n3/p2). Поскольку число итераций алгоритма совпадает с количеством процессоров, сложность параллельного алгоритма без учета затрат на передачу данных может быть определена при помощи выражения:
Tp = (n3/p2) * p = n3/p.
Показатели ускорения и эффективности данного параллельного алгоритма можно записать как:
S = Ts/Tp = n3 / ( n3 / p) = p
E = n3 / [ ( n3 / p) * p] = 1
Полученные показатели являются идеальными. На практике же мы обычно получаем относительные показатели, которые с идеальными не совпадают из-за затрат на выполнение операций передачи данных между процессорами, служебных затарт и пр.
Оценим реальные показатели с учётом затрат на выполнение операций передачи данных между процессорами. С учетом числа и длительности выполняемых операций время выполнения вычислений параллельного алгоритма может быть оценено следующим образом:
Tp(calc) = [ n2 / p ] * [ 2 n - 1 ] * t,
где t - время выполнения одной элементарной скалярной операции.
Для оценки коммуникационной сложности параллельных вычислений будем предполагать, что все операции передачи данных между процессорами в ходе одной итерации алгоритма могут быть выполнены параллельно. Объем передаваемых данных между процессорами определяется размером полос и составляет n/p строк или столбцов длины n. Общее количество параллельных операций передачи сообщений на единицу меньше числа итераций алгоритма (на последней итерации передача данных не является обязательной). Тем самым, оценка трудоемкости выполняемых операций передачи данных может быть определена как:
Tp ( comm ) = ( p - 1 ) * ( a + w * n * ( n / p ) / b ),
где a - латентность, b - пропускная способность сети передачи данных, а w - размер элемента матрицы в байтах. Тогда
Tp = ( n2 / p ) * ( 2 n - 1 ) * t + ( p - 1 ) * ( a + w * n * ( n / p ) / b ).
Демонстрация
Результаты вычислительных экспериментов
Производились перемножения матриц размером от 100x100 до 1000x1000 с шагом 100. Эксперимент проводился на 2-х и 4-х процессах на нетбуке Acer Aspire TimelineX 1830TZ со следующими характеристиками:
Intel Pentium Dual Core processor U5400 (1.2GHz, 3MB Cache)
Microsoft Windows 7 Домашняя базовая x64
Компилятор MS Visual Studio 2010
Порядок матрицы |
Последовательный алгоритм |
Параллельный алгоритм, 2 процесса |
Параллельный алгоритм, 4 процесса |
Время выполнения |
Время выполнения |
Ускорение |
Время выполнения |
Ускорение |
100 |
0,03100 |
0,01709 |
1,81392 |
0,01631 |
1,90067 |
200 |
0,21900 |
0,12541 |
1,74627 |
0,62880 |
0,34828 |
300 |
0,73300 |
0,27725 |
2,64382 |
0,69198 |
1,05927 |
400 |
1,71600 |
0,54128 |
3,17026 |
1,25752 |
1,36459 |
500 |
3,32300 |
0,95443 |
3,48165 |
1,87780 |
1,76962 |
600 |
5,74100 |
1,61671 |
3,55103 |
2,90378 |
1,97707 |
700 |
9,18800 |
2,57814 |
3,56380 |
4,41050 |
2,08321 |
800 |
13,68100 |
3,81406 |
3,58699 |
6,31865 |
2,16517 |
900 |
19,48400 |
5,39640 |
3,61055 |
8,86080 |
2,19889 |
1000 |
26,70700 |
7,35202 |
3,63260 |
11,76707 |
2,26963 |


Об авторе
Лабораторную работу выполнил студент группы 83-03 факультета ВМК: Стрельцов Максим



