Постановка задачи

Создать параллельную программу алгоритма Гаусса решения систем линейных алгебраических уравнений вида Ax=b с использованием его параллельной модификации с помощью MPI-библиотеки. Также нужно провести теоретический анализ эффективности алгоритма, провести эксперименты и сделать выводы.

Описание метода

Метод Гаусса - это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Приведение матрицы к треугольному виду называется прямым ходом метода Гаусса. Обратный ход начинается с решения последнего уравнения и заканчивается определением первого неизвестного.

Матрица A называется основной матрицей системы, b — столбцом свободных членов.Имеем Ax=b, где A=[aij] – матрица размерности n*n, det A>0, b=(a1, n+1, …, an, n+1)T. В простейшем случае алгоритм выглядит так:

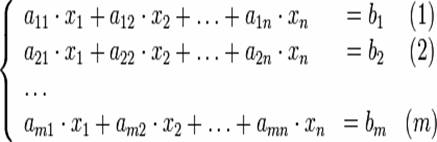
В предположении, что a11>0, первое уравнение системы:

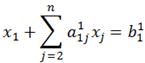
Затем из каждого из остальных уравнений вычитается первое уравнение, умноженное на соответствующий коэффициент ai1. В результате эти уравнения преобразуются к виду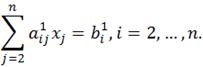

В результате последовательного исключения неизвестных система уравнений преобразуется в систему уравнений с треугольной матрицей:

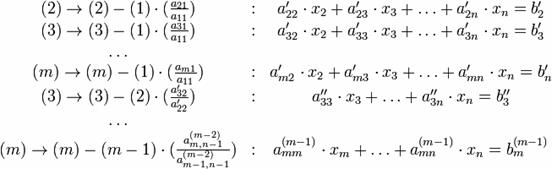
Совокупность проведенных действий называется прямым ходом метода Гаусса.Из n-го уравнения системы (2) определяем xn, из (n-1)-го – xn-1 и т.д. до x1. Совокупность таких действий называется обратным ходом метода Гаусса. Реализация прямого хода требует id=1397 арифметических операций, а обратного – id=1398 арифметических операций.

Демонстрация

Построение параллельного алгоритма решения методом Гаусса

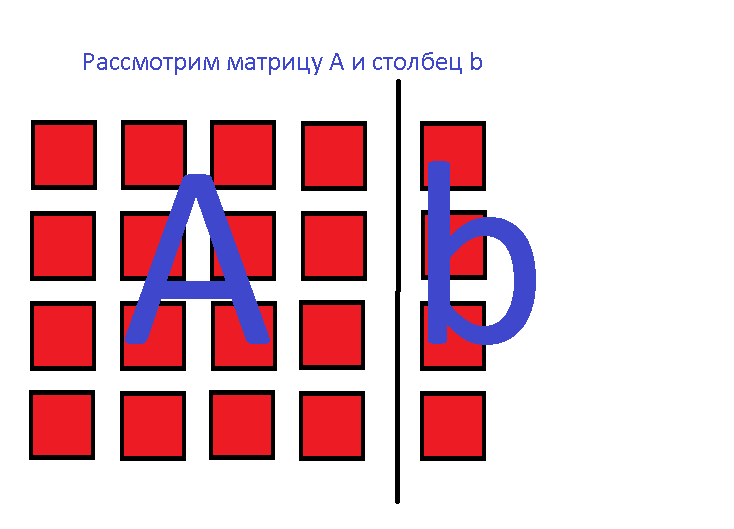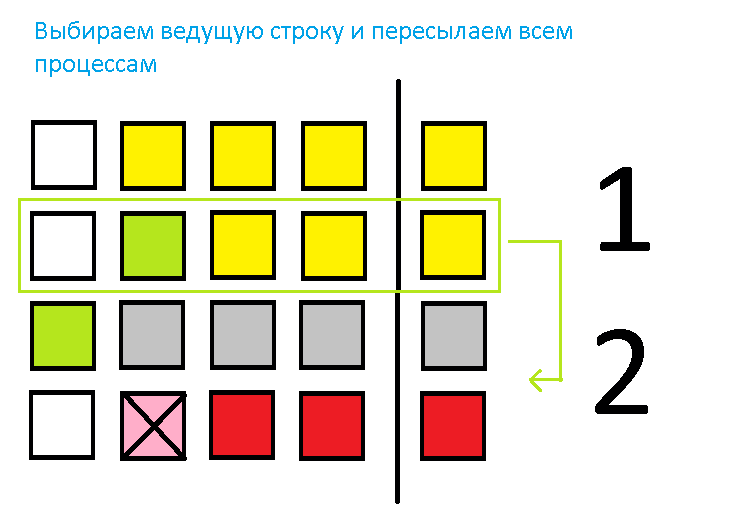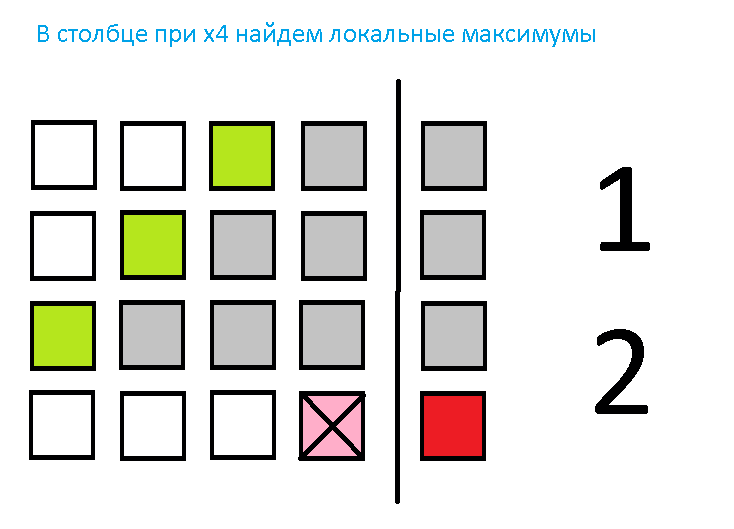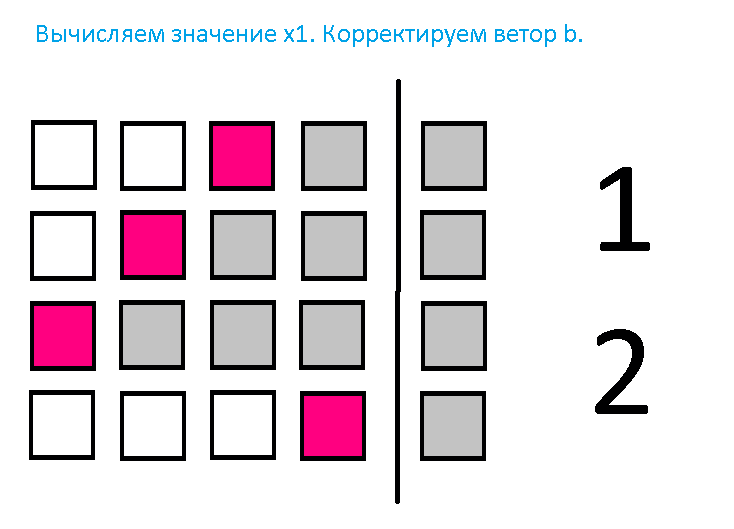
Поскольку решение методом Гаусса сводится к последовательности однотипных вычислительных операций умножения и сложения над строками матрицы, в качестве подзадач можно принять вычисления, связанные с обработкой одной или нескольких строк матрицы A и соответствующего элемента вектора b. Каждая итерация, связанная с решением очередной подзадачи, начинается с выбора ведущей строки. Ищется строка с наибольшим по абсолютной величине значением среди элементов i-го столбца, соответствующего исключаемой переменной xi. Поскольку строки матрицы A закреплены за разными подзадачами, для поиска максимального значения в столбце подзадачи с номерами k, должны обменяться элементами при исключаемой переменной xi. После сбора всех указанных коэффициентов может быть определено, какая из подзадач содержит ведущую строку и какое значение является ведущим элементом. Для продолжения вычислений ведущая подзадача должна разослать свою строку матрицы A и соответствующий элемент вектора b всем остальным подзадачам с номерами k, kxi. В обратном ходе метода Гаусса, как только какая-либо, например i–я подзадача, определила свою переменную xi, это значение рассылается всем подзадачам с номерами k. В каждой подзадаче полученное значение неизвестной умножается на соответствующий коэффициент и выполняется корректировка соответствующего элемента вектора b.

Анализ эффективности

Пусть n – порядок системы линейных уравнений, а p, p – число используемых процессоров, т.е. матрица А имеет размер n×n, а n/p – размер полосы на каждом процессоре (для простоты полагаем, что n/p – целое число). Определим сложность параллельного варианта метода Гаусса. В прямом ходе алгоритма для выбора ведущей строки на каждой итерации и каждом процессоре должно быть определено максимальное значение в столбце с исключаемой неизвестной в пределах закрепленной за ним полосы. По мере исключения неизвестных количество строк в полосах сокращается. После сбора полученных максимальных значений, определения и рассылки ведущей строки на каждом процессоре выполняется вычитание ведущей строки из каждой строки оставшейся части строк своей полосы матрицы A. Как мы установили выше, общие затраты на выполнение действий в одной строке на i-й итерации, составляет 2(n-i)+1 операций. Если применена циклическая схема распределения данных между процессорами, то на i-й итерации каждый процессор будет обрабатывать примерно (n-i)/p строк. Количество элементов строки, подлежащих обработке, также сокращается при исключении неизвестных, и текущее число элементов строки для вычислений оценивается величиной (n-i). Тем самым, сложность процедуры вычитания строк оценивается как 2(n-i) операций (перед вычитанием ведущая строка умножается на масштабирующую величину aik/aii ). С учетом выполняемого количества итераций общее число операций параллельного варианта прямого хода метода Гаусса определяется выражением:

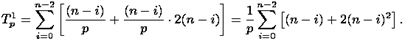
На каждой i-й итерации обратного хода после рассылки очередной вычисленной неизвестной на каждом процессоре обновляются значения правых частей для (n-i)/p еще не обработанных строк из числа закрепленных за ним n /p строк. Поскольку для каждой правой части выполняются 2 операции (умножение и вычитание), общее число операций, необходимых для обновления всех правых частей, составит:

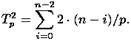
Таким образом суммарные затраты на реализацию прямого и обратного хода составят

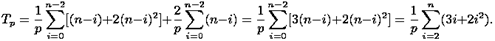
С использованием приближенных оценок вычислительной сложности последовательного и параллельного алгоритмов можно построить также оценки ускорения и эффективности:

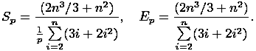
Полученные соотношения имеют достаточно сложный вид для оценивания. Вместе с тем можно показать, что сложность параллельного алгоритма имеет порядок ~(2n3/3)/p, и, тем самым, балансировка вычислительной нагрузки между процессорами в целом является достаточно равномерной.

Дополним сформированные показатели вычислительной сложности метода Гаусса оценкой затрат на выполнение операций передачи данных между процессорами. При выполнении прямого хода на каждой итерации для определения ведущей строки процессоры обмениваются локально найденными максимальными значениями в столбце с исключаемой переменной. Выполнение данного действия одновременно с определением среди собираемых величин наибольшего значения может быть обеспечено при помощи операции обобщенной редукции (функция MPI_Allreduce библиотеки MPI ). Всего для выполнения такой операции требуется log2p шагов, что с учетом количества итераций позволяет оценить время, необходимое для проведения операций редукции, при помощи следующего выражения:

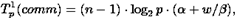
где, как и ранее, α – латентность сети передачи данных, β – пропускная способность сети, w – размер пересылаемого элемента данных.

Далее также на каждой итерации прямого хода метода Гаусса выполняется рассылка выбранной ведущей строки. Сложность данной операции передачи данных:

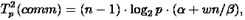
При выполнении обратного хода алгоритма Гаусса на каждой итерации осуществляется рассылка между всеми процессорами вычисленного значения очередной неизвестной. Общее время, необходимое для выполнения подобных действий, можно оценить как:

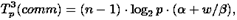
В итоге, с учетом всех полученных выражений, трудоемкость параллельного варианта метода Гаусса составляет:

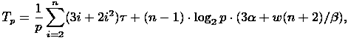
где τ есть время выполнения базовой вычислительной операции.

Результаты экспериментов

Intel(R) Pentium(R) Dual CPU T3200 @ 2.00GHz 2.00GHz

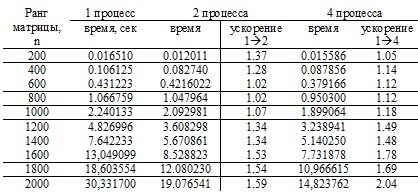
Intel(R) Pentium(R) Dual CPU T3200 @ 2.00GHz 2.00GHz

Intel(R) Pentium(R) Dual CPU T2390 @ 1.86GHz 1.87GHz

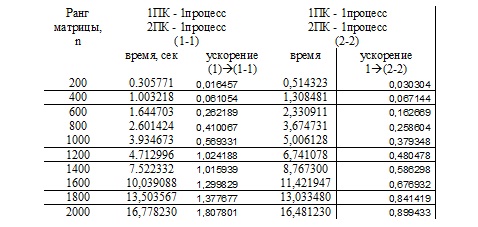
Выводы

Из результатов проведенных экспериментов,видно,что при вычислениях (на одном компьютере) с числом процессов, равным числу ядер ЦП (2 ядра),ускорение вычислений происходит пркатически сразу. При увеличении числа процессов происходит замедление скорости вычислений.Таким образом, эффективнее использовать число процессов равное числу ЦП (или ядер) на компьютере.

При выполнении расчетов на процессах, запущенных на двух кмопьютерах, также получаем ускорение большее единицы, как и при вычислнениях описанных выше, но не сразу. При маленькой размерности матрицы – вариант,когда на каждом компьютере запущено по 1 процессу (1 процесс-1 процесс) уступает локальному (2 процесса) из-за накладных расходов, связанных с передачей информации по сети. Если же рассматривать вариант, когда на каждом компьютере запущено по 2 процесса(2 - 2), то этот вариант эффективен только при больших размерах матрицы, т.е. когда время на пересылку данных по сети становится менее значимым по сравнению со временем, потраченным на непосредственные вычисления.

Об авторах

Васильев Федор и Голомидов Филипп
группа 8410