Отчет

Постановка задачи

Задача состоит в решении системы линейных уравнений вида:

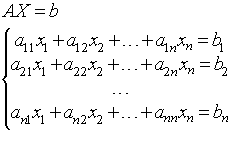
Матрица А размера (NxN) невырожденная. Для решения используется итеративный метод Якоби. Для этого исходная система заменяется эквивалентной:

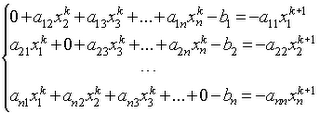
В начале делается некоторое начальное предположение X0, обычно равное вектору B=[b1/a11, ... ,bi/aii, ... ,bn/ann], т.е. Х0=В; затем метод генерирует на каждом шаге последовательность аппроксимаций Xk , k=1,2,3,... Для их вычисления используется следующая итеративная формула:

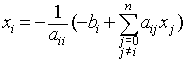
В общем случае итерации могут не сходится, тем не менее если система строго диагонально доминирующая то итерации будут сходится. Критерием окончания итерационного процесса может являться следующая проверка:

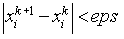
Параллельный алгоритм

Оценим трудоемкость рассмотренного параллельного варианта метода Якоби. Пусть, как и ранее, N есть порядок решаемой системы линейных уравнений, а p, p 1) Размер матрицы (Size).
2) Начальное приближение вектора X (x0).
3) Строки матрицы A и элементы вектора b, необходимые для вычисления соответствующего подвектора xk.

После получения необходимой информации каждый процессор будет вычислять соответствующие компоненты вектора X. И передавать их главному процессору. В свою очередь главный процессор при получении очередного приближения решения Xk должен сравнить его с предыдущим приближением Xk-1. И если норма разности этих векторов окажется меньше заданной точности (eps), то вычисления закончатся. В противном случае вектор Xk будет разослан по всем процессам и будет вычисляться очередное приближение решения.

Демонстрация работы параллельного алгоритма

Выполнение k+1-ой итерации происходит по следующей схеме:

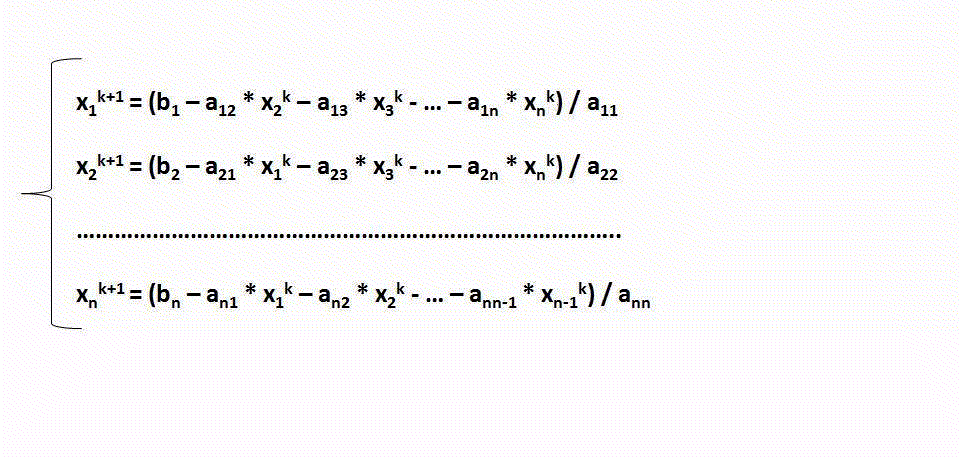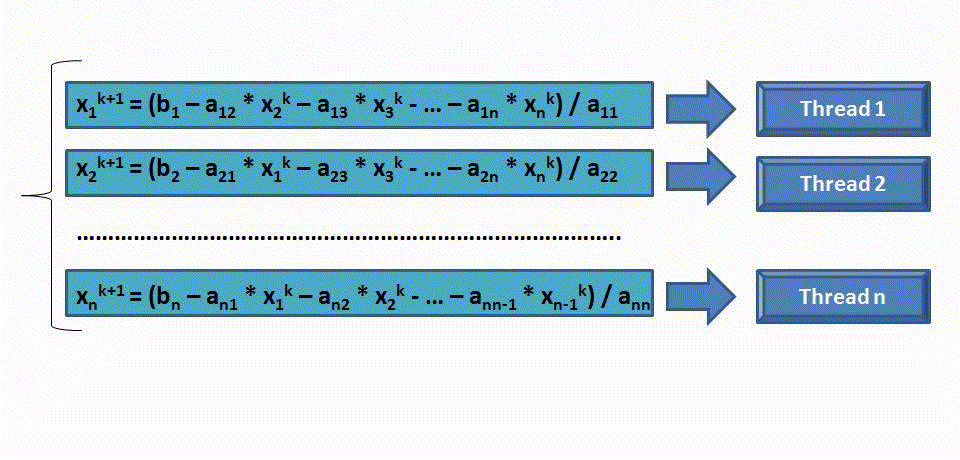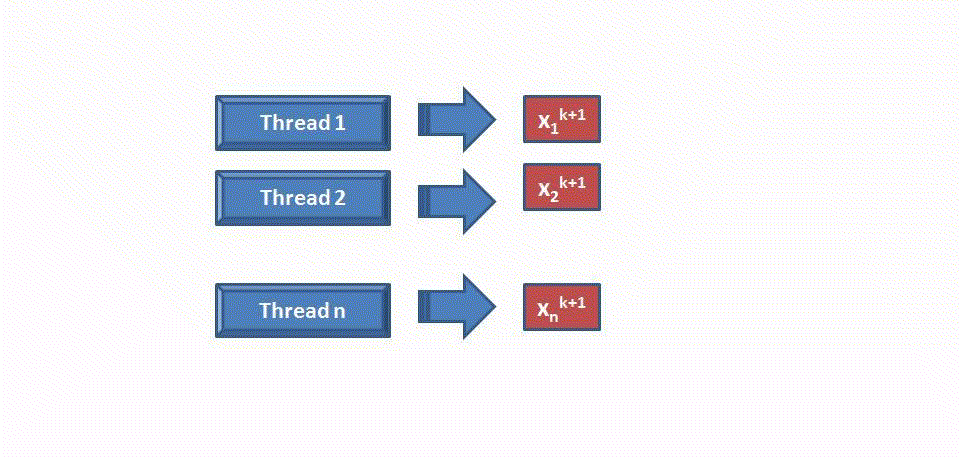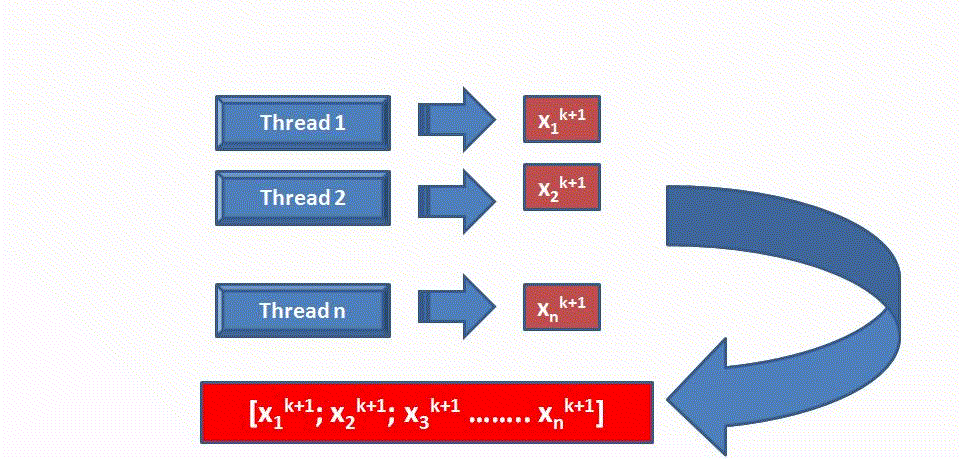
Анализ эффективности

Время, затраченное на последовательное выполнение алгоритма, выражается следующей формулой:
T = k * (2*n^2 - n), где k – число выполненных итераций, а n – число уравнений.

Время, затраченное на параллельное выполнение алгоритма на p процессорах без учета затрат на передачу данных, выражается формулой:
T(p) = k/p * (2*n^2 - n)

Тогда ускорение равно:
S = T(1) / T(p) = p

Эффективность:
E = T1 / p*Tp = 1

Разработанный способ параллельных вычислений позволяет достичь идеальных показателей ускорения и эффективности.

Определим время, затрачиваемое на передачу данных. Для этого используем модель Хокни.

Первоначальная рассылка данных требует следующее время:
Tcomm1 = (p-1) * (4*alfa + (n^2 / p + n) / betta), где alfa - латентность, betta - пропускная способность сети

Передача данных, выполняемая в итерационном процессе, затрачивает следующее время:
Tcomm2 = k * (p-1) * (3*alfa + (n / p + n) / betta), где k - количество выполненных итераций

В итоге общее время передачи данных выражается формулой:
Tcomm = (p-1) * (4*alfa + (n^2 / p + n) / betta) + k * (p-1) * (3*alfa + (n / p + n) / betta)

Это время зависит от числа итераций. Как правило, их количество меньше числа уравнений n. Значит время на передачу данных можно оценить величиной:
Tcomm = O(n^2)
В свою очередь и ко времени выполнения алгоритма применима та же оценка:
T = O(n^2)

Если число итераций будет сравнимо с n, то для времени выполнения алгоритма будет справедлива уже другая оценка:
T = O(n^3)

Результаты экспериментов

Эксперименты проводились на следующей машине:
Intel Core-i5-2410M CPU @ 2.3GHz

Время работы алгортимов и полученные ускорения представлены в таблице1:

Таблица 1. Ускорение вычислений

Размер матрицы

Количество итераций

Последовательный

Параллельный
(2 процесса)

Ускорение
(2 процесса)

Параллельный
(4 процесcа)

Ускорение
(4 процесса)

500 * 500

3662

3.6

1.8

2

1.7

2.1

1000 * 1000

7441

31.4

16.1

1.95

14.4

2.18

2000 * 2000

13991

235.4

118.9

1.97

107.6

2.18

Из полученных данных видно, что параллельная работа алгоритма дает замедление. Это связано с накладными расходами на передачу данных между процессорами.Также при обмене данными требуется синхронизировать работу процессоров, что тоже не улучшает производительность.

В таблице 2 приведены теоретическое и экспериментальное время:

Таблица 2. Сравнение теоретических оценок и экспериментальных данных.

Размер матрицы

Теоретическое время
(2 процесса)

Экспериментальное время
(2 процесса)

Теоретическое время
(4 процесса)

Экспериментальное время
(4 процесса)

500 * 500

1.8

1.8

0.9

1.7

1000 * 1000

15.7

16.1

7.9

14.4

2000 * 2000

117.7

118.9

58.6

107.6

Как видно из приведённых результатов при локальных вычислениях (на одном компьютере) с числом процессов, равным числу ядер ЦП (2 ядра), выигрыш во времени происходит практически сразу и ускорение достаточно близко к идеальному (идеальное ускорение на двух ядрах = 2). При вычислениях в 4 процесса получаем наоборот – замедление. Это связано с дополнительными коммуникационными расходами при передаче данных между большим числом процессов. Из полученных данных видно, что параллельная работа алгоритма дает замедление. Это связано с накладными расходами на передачу данных между процессорами и разделением времени ЦП. Также при обмене данными требуется синхронизировать работу процессоров, что тоже не улучшает производительность.

Об авторах