Постановка задачи

В поставленную задачу входит реализация параллельной программы перемножения матриц по алгоритму Кэннона при блочном разделении данных. Необходимо провести эксперименты и на их основании сделать выводы, а также провести анализ эффективности алгоритма.

Описание последовательного алгоритма

Умножение матрицы A размера m×n и матрицы B размера n×l приводит к получению матрицы С размера m×l, каждый элемент которой определяется в соответствии с выражением:

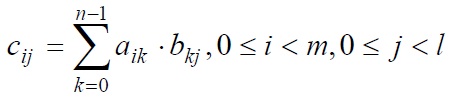
Значит каждый элемент результирующей матрицы С есть скалярное произведение соответствующих строки матрицы A и столбца матрицы B:

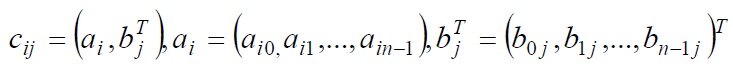
Этот алгоритм предполагает выполнение m*n*l операций умножения и столько же операций сложения элементов исходных матриц. При умножении квадратных матриц размера n×n количество выполненных операций имеет порядок O(n³). Также будем предполагать далее, что все матрицы являются квадратными и имеют размер n×n. Последовательный алгоритм умножения матриц представляется тремя вложенными циклами:

Этот алгоритм является итеративным и ориентирован на последовательное вычисление строк матрицы С. При выполнении одной итерации внешнего цикла (цикла по переменной i) вычисляется одна строка результирующей матрицы:

Поскольку каждый элемент результирующей матрицы есть скалярное произведение строки и столбца исходных матриц, то для вычисления всех элементов матрицы С размером n×n необходимо выполнить n²*(2n-1) скалярных операций и затратить время T₁= n²*(2n-1)*r, где r – есть время выполнения одной элементарной скалярной операции.

Описание параллельного алгоритма. Выделение информационных зависимостей. Масштабирование и распределение подзадач по процессорам

Для многих методов матричных вычислений характерным является повторение одних и тех же вычислительных действий для разных элементов матриц. Данный момент свидетельствует о наличии параллелизма по данным при выполнении матричных расчетов и, как результат, распараллеливание матричных операций сводится в большинстве случаев к разделению обрабатываемых матриц между процессорами. Выбор способа разделения матриц приводит к определению конкретного метода параллельных вычислений. В данной работе рассмотрен способ разбиения матриц на прямоугольные фрагменты (блоки).

При блочном разделении матрица делится на прямоугольные наборы элементов – при этом, как правило, используется разделение на непрерывной основе. Пусть количество процессоров составляет p=s*q, количество строк матрицы является кратным s, а количество столбцов – кратным q, то есть m=k*s и n=l*q.

Представим исходную матрицу A в виде набора прямоугольных блоков следующим образом:

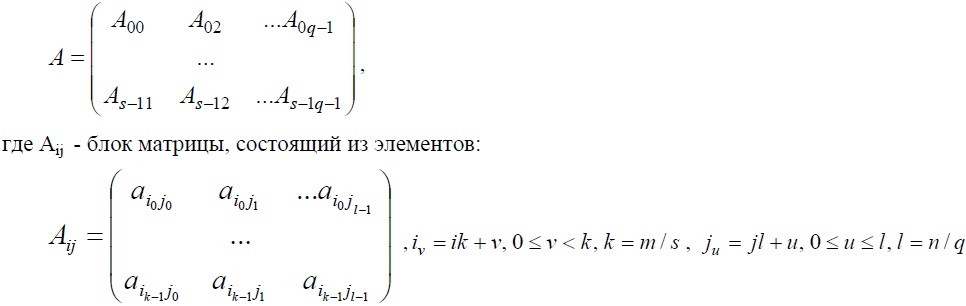
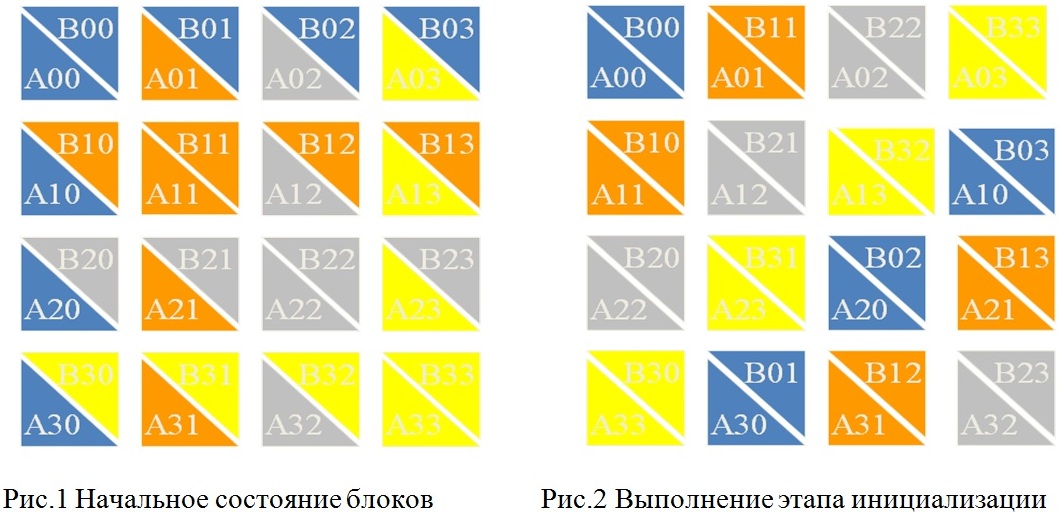
Начальное расположение блоков в алгоритме Кэннона подбирается таким образом, чтобы располагаемые блоки в подзадачах могли бы быть перемножены без каких-либо дополнительных передач данных.

Алгоритм состоит из двух этапов - это этап инициализации алгоритма и его основной цикл.

Этап инициализации алгоритма Кэннона включает выполнение следующих операций передач данных:

• в каждую подзадачу (i,j) передаются блоки A_ij, B_ij;
• для каждой строки i решетки подзадач блоки матрицы A сдвигаются на (i-1) позиций влево;
• для каждого столбца j решетки подзадач блоки матрицы B сдвигаются на (j-1) позиций вверх.

Выполняемые при перераспределении матричных блоков процедуры передачи данных являются примером операции циклического сдвига.

Основной цикл алгоритма Кэннона включает выполнение следующих операций:

• циклический сдвиг влево блоков строки
• циклический сдвиг вверх блоков столбца

Тогда алгоритм выглядит:

• Все строки (кроме первой) циклически сдвигаем влево
• Все столбцы (кроме первого) циклически сдвигаем вверх
• Вычисляем С[i,j]=C[i,j]+A[i,j]*B[i,j]
• for(i = 0, i < n, i++)
  • Все строки циклически сдвигаем влево
  • Все столбцы циклически сдвигаем вверх
  • Вычисляем С[i,j]=C[i,j]+A[i,j]*B[i,j]

В рассмотренной схеме параллельных вычислений количество блоков может варьироваться в зависимости от выбора размера блоков – эти размеры могут быть подобраны таким образом, чтобы общее количество базовых подзадач совпадало с числом процессоров p. Так, например, в наиболее простом случае, когда число процессоров представимо в виде p=δ² (т.е. является полным квадратом) можно выбрать количество блоков в матрицах по вертикали и горизонтали равным δ (т.е. q=δ). Такой способ определения количества блоков приводит к тому, что объем вычислений в каждой подзадаче является одинаковым и, тем самым, достигается полная балансировка вычислительной нагрузки между процессорами.

В этом случае, для распределения подзадач между процессорами можно осуществить непосредственное отображение набора подзадач на множество процессоров т.е. базовую подзадачу (i,j) следует располагать на процессоре P_i,j.

Далее для наглядности рассмотрим вычисления на процессоре P_1,2

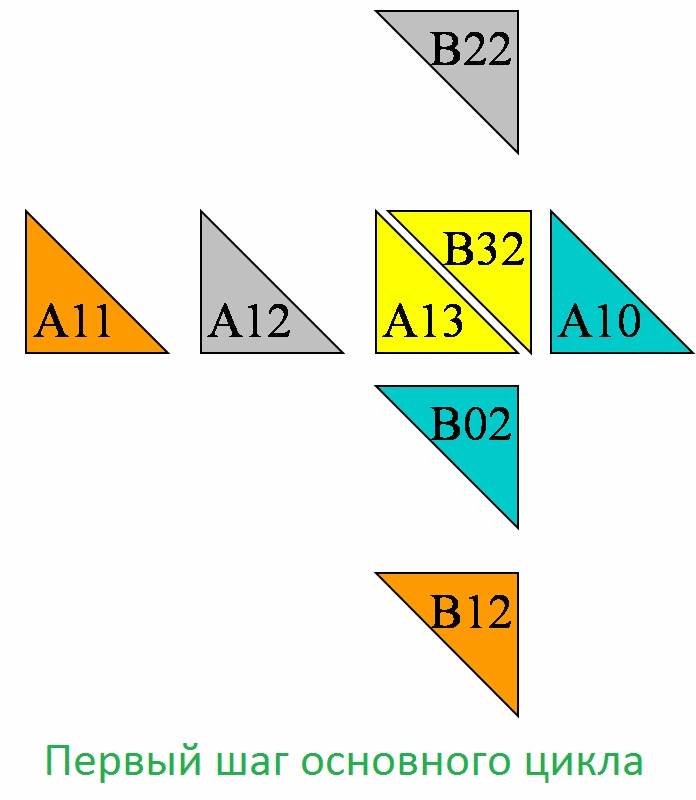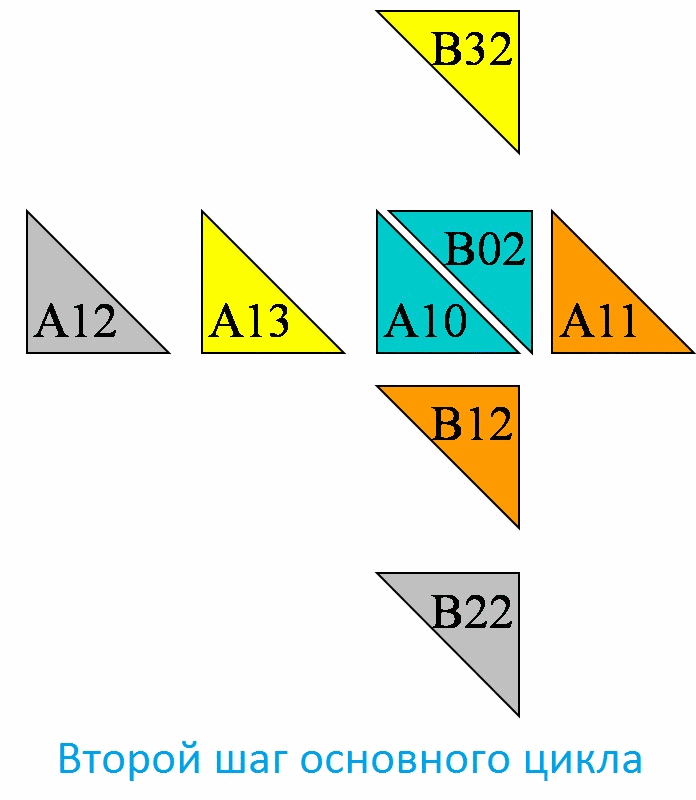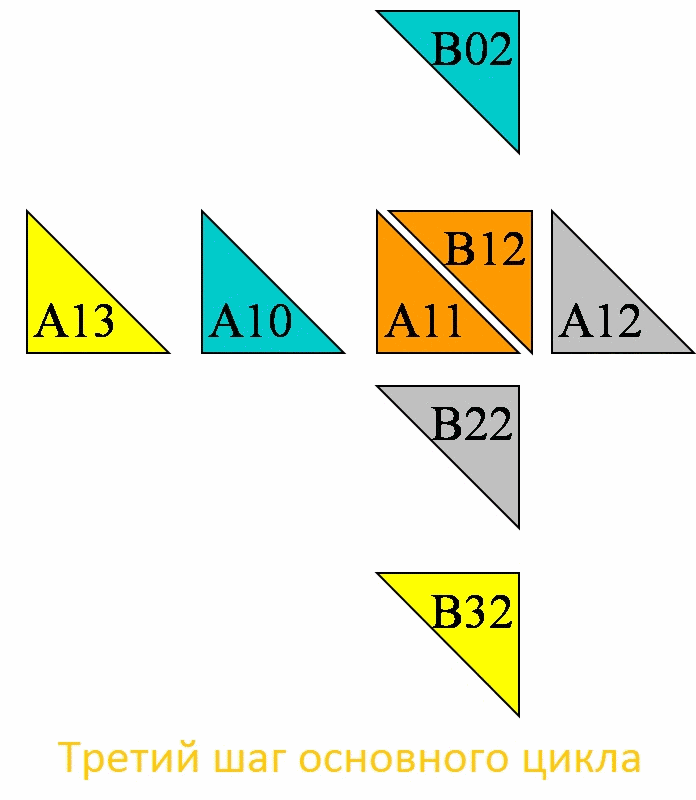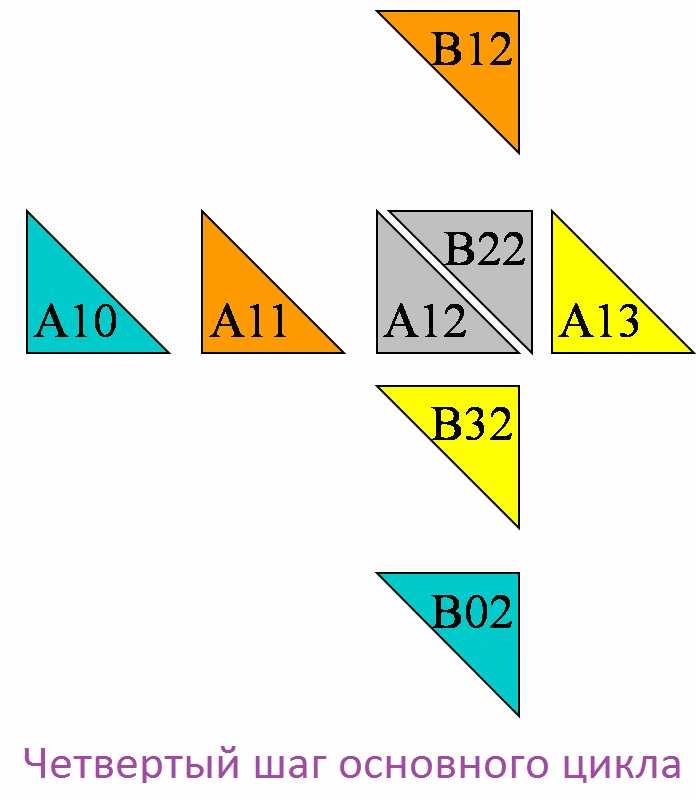
В результате проделанных на процессоре P_1,2 четырех шагов, в соответствующей ячейки матрицы C получили следующее значение: C[1,2]=A[1,3]*B[3,2]+ A[1,0]*B[0,2]+ A[1,1]*B[1,2]+ A[1,2]*B[2,2].

Анализ эффективности

Время выполнения вычислительных операций алгоритма Кэннона:

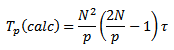
, где τ – время выполнение одной элементарной скалярной операции

Трудоемкость выполняемых операций передачи данных может быть определена как:

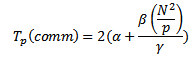
, где α – латентность, γ – пропускная способность сети передачи данных, а β есть размер элемента матрицы в байтах

С учетом полученных соотношений общее время выполнения параллельного алгоритма матричного умножения определяется следующим выражением:

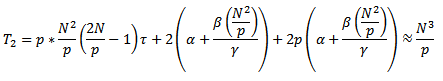
Рассчитаем ускорение по формуле:

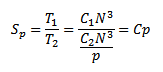
Эффективность алгоритма составит:

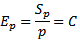
Результаты вычислительных экспериментов

Конфигурация оборудования:

Intel i5 M450 2400 Мгц 
Cache: L1 ‒  32 Kb, L2 ‒  64 Kb, L3 ‒  4Mb
RAM:  4Gb, DDR3 1333 MHz
Compiler: MS Visual Studio 2005

Результаты измерений при запуске в 4 процесса:

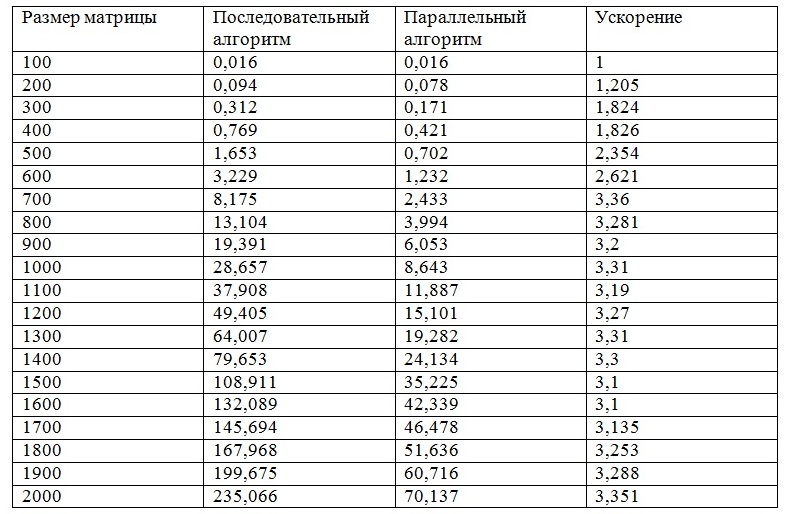
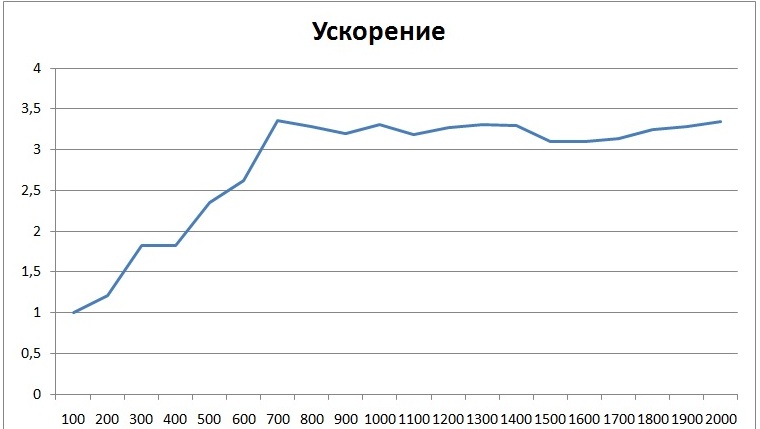
График зависимости ускорения от размера матриц:

Для оценки длительности τ базовой скалярной операции проводилось решение задачи умножения матриц при помощи последовательного алгоритма и полученное таким образом время вычислений делилось на общее количество выполненных операций – в результате подобных экспериментов для величины τ было получено значение 17,8 нсек.

Сравнение экспериментального и теоретического времени выполнения параллельного алгоритма Кэннона:

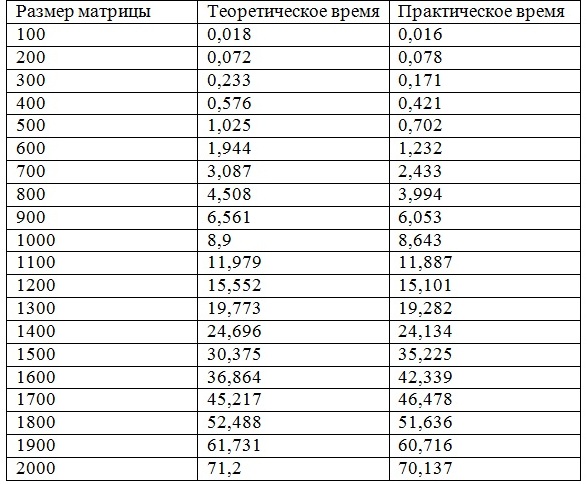
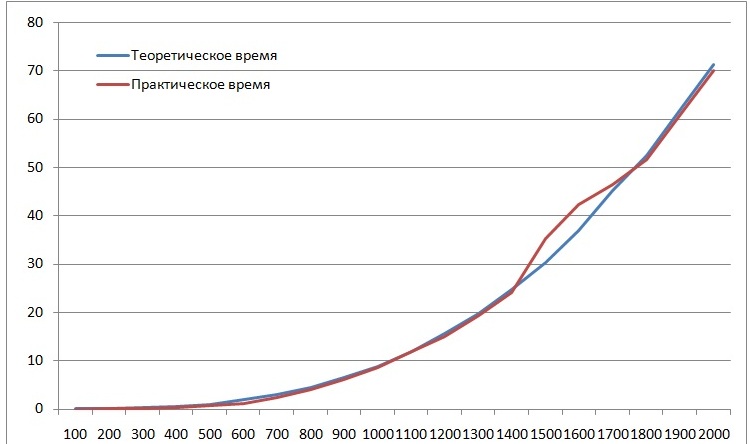
График зависимости времени от размера матриц:

Вывод

В результате проведенных экспериментов были подтверждены теоретические временные оценки работы алгоритма Кэннона. На графике видно, что они практически совпадают. На размере матриц 1500*1500 время работы алгоритма отличается от теоретического, это связанно с более удачным расположением данных в кэш-памяти на процессоре.

Об авторах

Сурьянинова Ольга группа 8409 и Мечетин Иван группа 8410