Рассмотрим умножение матрицы А на матрицу В, результатом которого будет матрица С, т.е.
AxB=C.
________________________________________
Случай p = n2
________________________________________
В этом случае каждый процессор получает по одному элементу от каждой из матриц А, В и С. Обозначим процессор с номером i*n+j как pi,j, элементы матриц А, В, С, стоящие в i-ой строке j-ом столбце соответственно ai,j, bi,j, ci,j. Тогда элементы матриц будут распределены между процессорами следующим образом:
for (int i=0; i < n; i++)
for (int j=0; j < n; j++)
процессор pi,j получает элементы ai,j, bi,j, ci,j.
В данном частном случае Fox's алгоритм будет выполнять умножение матриц А и В за n этапов. Пусть начальный этап имеет номер 0, а последний - n-1.
Этап 0.
for (int i=0; i < n; i++)
for (int j=0; j < n; j++)
для процессора pi,j: ci,j, = ai,i * bi,j,
т.е. процессор pi,j умножает диагональный элемент ai,i матрицы А на элемент bi,j матрицы В, а результат умножения помещает в элемент ci,j матрицы С.
Таким образом, процессор pi,j должен иметь доступ к элементу ai,i матрицы А. Это будет достигнуто за счет возможности обмена данными между процессорами.
Введем понятие деления по модулю n:
i mod n = i, если i < n
i mod n = i % n, если i > = n ( i % n - остаток от деления i на n )
Этап 1.
for (int i=0; i < n; i++)
for (int j=0; j < n; j++)
для процессора pi,j: ci,j += ai,(i+1) mod n * b(i+1) mod n,j,
Элемент ai,(i+1) mod n матрицы А - элемент, стоящий непосредственно справа от диагонального элемента ai,i, если это возможно, иначе – первый элемент текущей строки. В случае матрицы 4-го порядка это будет выглядеть следующим образом:
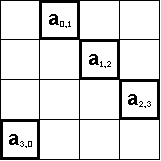
Элемент b(i+1) mod n,j матрицы В - это элемент стоящий на одну строчку ниже в отличии от элемента bi,j этапа 0, для последней строки матрицы В – первая строка матрица В.
Этап k (k=2,n-1).
for (int i=0; i < n; i++)
for (int j=0; j < n; j++)
для процессора pi,j: ci,j += ai,(i+k) mod n * b(i+k) mod n,j,
После выполнения последнего этапа алгоритма Фокса элемент ci,j будет представляться в виде следующей суммы:
ci,j = ai,i * bi,j + ai,i+1 * bi+1,j +...+ ai,n-1 * bn-1,j + ai,0 * b0,j +...+ ai,i-1 * bi-1,j,
которая является суммой произведений элементов i-ой строки матрицы А на элементы j-го столбца матрицы В. Это доказывает правильность алгоритма Фокса для перемножения квадратных матриц порядка n и числа процессоров p = n2.
________________________________________
Случай p < n2
________________________________________
На практике требование p = n2 является трудно выполнимым. Решением данной проблемы является назначение процессорам не отдельных элементов, а квадратных подматриц порядка n/(p1/2) от каждой из матриц A, B и С. В этом случае алгоритм Фокса будет выполнять умножение матриц А и В за p1/2 этапов.
В соответствии с алгоритмом Фокса в ходе вычислений на каждом процессоре pi,j располагается четыре матричных блока:
• блок Сi,j матрицы С, вычисляемый процессором;
• блок Аi,j матрицы A, размещаемый в подзадаче перед началом вычислений;
• блоки А’i,j, В’i,j матриц A и B, получаемые подзадачей в ходе выполнения вычислений.
Выполнение параллельного метода включает:
• этап инициализации, на котором каждому процессору pi,j передаются блоки Аi,j, Вi,j и обнуляются блоки Сi,j на всех подзадачах;
• этап вычислений, в рамках которого на каждой итерации l,0<=l< p1/2, осуществляются следующие операции:
• для каждой строки i, 0<=i< p1/2, блок Аi,j процессора pi,j пересылается на все подзадачи той же строки i решетки; индекс j, определяющий положение подзадачи в строке, вычисляется в соответствии с выражением
j=(i+l) mod p1/2;
• полученные в результате пересылок блоки Аi,j, В’i,j каждого процессора pi,j перемножаются и прибавляются к блоку Сi,j
• блоки В’i,j каждого процессора pi,j пересылаются процессорам, являющимся соседями сверху в столбцах решетки процессоров (блоки процессоров из первой строки решетки пересылаются процессорам последней строки решетки).
Таким образом, все происходит аналогично алгоритму, описанному в предыдущем случае, за той лишь разницей, что вместо элементов ai,j, bi,j, ci,j мы рассматриваем соответственно подматрицы Аi,j, Вi,j, Сi,j. Все формулы и все описания этапов остаются прежними, за исключением того, что вместо n везде используем p1/2 .
Однако то, что p1/2 и n/(p1/2) мы приняли за целые числа, не всегда является верным. Первую проблему можно решить следующим образом: из общего числа процессоров взять только то число, из которого извлекается корень, а оставшиеся процессоры будут неработающими. Во втором случае трудности, связанные с порядком матриц можно преодолеть за счет введения недостающих строк и столбцов, заполненных нулевыми элементами. В дальнейшем будем полагать, что n/(p1/2) - целое число.
Анализ эффективности
________________________________________
Определим вычислительную сложность данного алгоритма. Построение оценок будет происходить при условии выполнения всех ранее выдвинутых предположений - все матрицы являются квадратными размера n×n, количество блоков по горизонтали и вертикали являются одинаковым и равным q= p1/2 (p – количество процессоров) (т.е. размер всех блоков равен k×k, где k=n/q), процессоры образуют квадратную решетку.
Алгоритм Фокса требует для своего выполнения q итераций, в ходе которых каждый процессор перемножает свои текущие блоки матриц А и В и прибавляет результаты умножения к текущему значению блока матрицы C.
С учетом выдвинутых предположений общее количество выполняемых при этом операций будет иметь порядок n3/p.
Как результат, показатели ускорения и эффективности алгоритма имеют вид:
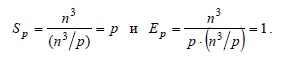
Уточним полученные соотношения — для этого укажем более точно количество вычислительных операций алгоритма и учтем затраты на выполнение операций передачи данных между процессорами.
Определим количество вычислительных операций. Сложность выполнения скалярного умножения строки блока матрицы A на столбец блока матрицы В можно оценить как 2(n/q)-1. Количество строк и столбцов в блоках равно n/q и, как результат, трудоемкость операции блочного умножения оказывается равной (n2/p)(2n/q-1). Для сложения блоков требуется n2/p операций. С учетом всех перечисленных выражений время выполнения вычислительных операций алгоритма Фокса может быть оценено следующим образом:
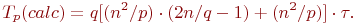
, где τ - время выполнения одной элементарной скалярной операции.
Оценим затраты на выполнение операций передачи данных между процессорами. На каждой итерации алгоритма перед умножением блоков один из процессоров строки процессорной решетки рассылает свой блок матрицы A остальным процессорам своей строки.
Как результат, время выполнения операции передачи блоков матрицы A может оцениваться как:
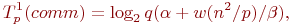
где α – латентность, β – пропускная способность сети передачи данных, а w есть размер элемента матрицы в байтах. В случае же когда топология строк процессорной решетки представляет собой кольцо, выражение для оценки времени передачи блоков матрицы A принимает вид:
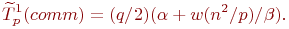
Далее после умножения матричных блоков процессоры передают свои блоки матрицы В предыдущим процессорам по столбцам процессорной решетки. Эти операции могут быть выполнены процессорами параллельно и, тем самым, длительность такой коммуникационной операции составляет:
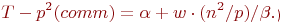
Просуммировав все полученные выражения, можно получить, что общее время выполнения алгоритма Фокса может быть определено при помощи следующих соотношений:
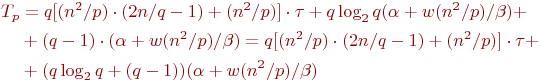
Демонстрация
________________________________________
Рассмотрим работу алгоритма Фокса на примере умножения матриц 4-го порядка на 4-х процессорах, то есть n=4, p=4. В этом случае каждому процессору назначается подматрица порядка n/(p1/2) = 2 от каждой из матриц А, В и С и алгоритм Фокса выполняет умножение матриц за p1/2 = 2 этапа:
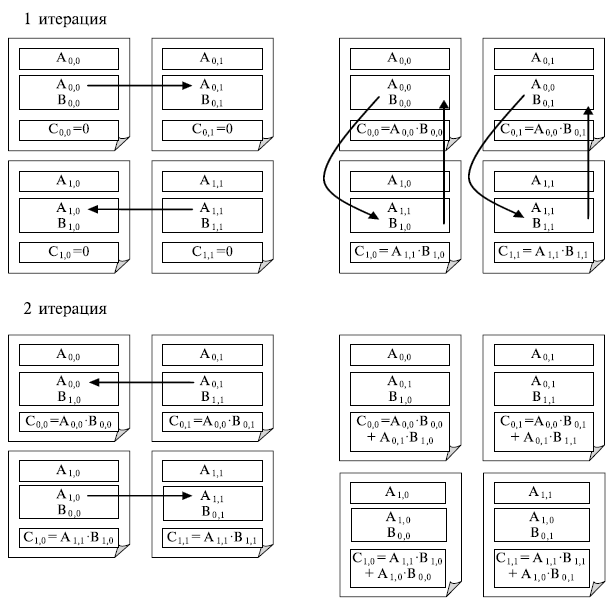
На данных рисунках проиллюстрировано перемещение блоков Ai,j и Bi,j между процессорами Pi,j.
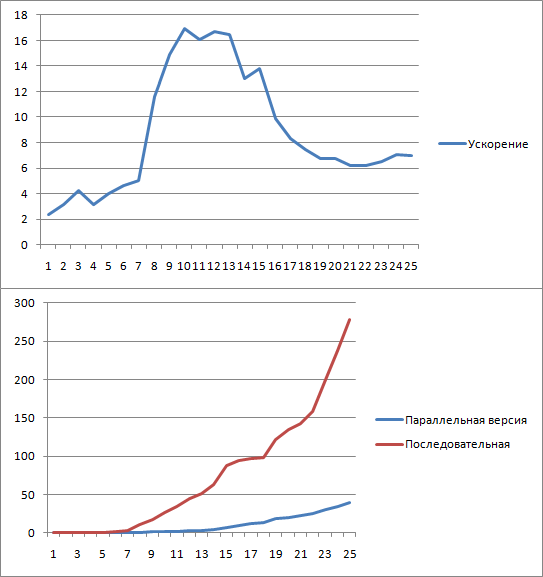
Результаты вычислительных экспериментов
________________________________________
Производились умножения квадратных матриц размером 100x100 с шагом 100 до 2500x2500. Эксперименты проводились на машине со следующей конфигурацией:
Processor: Mobile QuadCore Intel Core i7 2670QM @ 2.2GHz (3.1 GHz Turbo Boost)
Cache: L1 ‒ 256 Kb, L2 ‒ 1 Mb, L3 ‒ 6Mb
RAM: 4Gb, DDR3 1333 MHz
Разработка программ проводилась в среде Microsoft Visual Studio 2010, для компиляции использовался стандартный компилятор, предоставляемый средой, с включенной полной оптимизацией.
Напыльникова Я. Лебедев С. gr 83 - 03



