Постановка задачи
В любое время ценился порядок в чем-либо. Однако сейчас информации стало настолько много, что для её поиска требуется огромное количество времени. В большинстве случаев обработка данных есть совокупность двух основных частей: сортировки и поиска. Если возникает потребность найти какие-либо данные из огромного списка, то на это может уйти очень много времени. Значит, нужно их расположить так, чтобы их было проще найти. Отсюда вытекает проблема сортировки того или иного набора данных.
Существует множество различных алгоритмов сортировки, но самый простой из них это сортировка пузырьком. К сожалению, он также один из самых медленных. Избавиться от этого недостатка помогает алгоритм параллельной пузырьковой сортировки, который мы и ставим целью реализовать.
В работе требуется реализовать параллельный алгоритм сортировки пузырьком ,а так же сравнить время выполнения последовательного и параллельного алгоритмов.
Метод решения
Последовательный алгоритм пузырьковой сортировки сравнивает и обменивает соседние элементы в последовательности, которую нужно отсортировать. Для последовательности
(a1, a2, ..., an)
алгоритм сначала выполняет n-1 базовых операций "сравнения-обмена" для последовательных пар элементов
(a1, a2), (a2, a3), ..., (an-1, an).
В результате после первой итерации алгоритма самый большой элемент перемещается ("всплывает") в конец последовательности. Далее последний элемент в преобразованной последовательности может быть исключен из рассмотрения, и описанная выше процедура применяется к оставшейся части последовательности
(a'1, a'2, ..., a'n-1).
Параллельная схема
Сортируемый массив разбивается на p равных частей. В каждой части содержится n/p элементов. Полученные блоки рассылаются по процессам. Каждый процесс сортирует свою часть массива методом последовательной пузырьковой сортировки. Далее происходит чередование чет-нечетных перестановок на p итерациях. На нечетных итерациях пары процессов с номерами (0,1)(2,3)(4,5)… обмениваются друг с другом массивами и сортируют их заново. На четной итерации происходит обмен между процессами с номерами (1,2)(3,4)(5,6)(7,8)… . В общем случае выполнение параллельного метода может быть прекращено, если в течение каких-либо двух последовательных итераций сортировки состояние упорядочиваемого набора данных не было изменено.
Анализ эффективности
Определим первоначально трудоемкость последовательных вычислений. Трудоёмкость последовательного алгоритма пузырьковой сортировки имеет вид
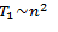
Определим теперь сложность рассмотренного параллельного алгоритма упорядочивания данных. Как отмечалось ранее, на начальной стадии работы метода каждый процессор проводит упорядочивание своих блоков данных (размер блоков при равномерном распределении данных равен n/p ). Данная начальная сортировка выполняется при помощи сортировки пузырьком, тогда трудоемкость начальной стадии вычислений можно определить выражением вида:
 .
.
Далее, на каждой выполняемой итерации параллельной сортировки взаимодействующие пары процессоров осуществляют передачу блоков между собой, после чего получаемые на каждом процессоре пары блоков объединяются при помощи процедуры слияния. Общее количество итераций не превышает величины p, и, как результат, общее количество операций этой части параллельных вычислений оказывается равным
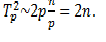
С учетом полученных соотношений показатели эффективности и ускорения параллельного метода сортировки имеют вид:
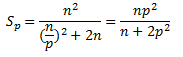
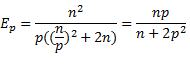
Результаты вычислительных экспериментов

Конфигурация системы:
Тип ЦП - Mobile DualCore Intel Pentium T4200, 1600 MHz
Число ядер - 2
Оперативная память - 8023 Мб
Операционная система - Microsoft Windows XP Professional
Компилятор - MS Visual Studio 2010
Об авторе
Работу выполнила студентка группы 83-03 Пашко Алена



