|
|
 |
 Отчет
Отчет по лабораторной работе по курсу "Многопроцессорные вычислительные системы и параллельное программирование"
Тема "Решение системы СЛУ итеративным методом Якоби"
Выполнили студенты группы 84-10 Штыркова О.А., Сериков Е.В.
- Постановка задачи
Дана система линейных уравнений:
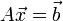 ,
где ,
где
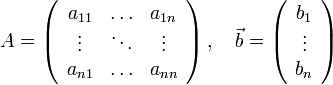
Или
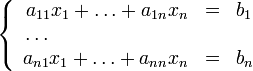
Для того, чтобы построить итеративную процедуру метода Якоби, необходимо провести предварительное
преобразование системы уравнений 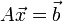 к итерационному виду к итерационному виду 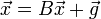 .
Это преобразование осуществляется по следующему правилу: .
Это преобразование осуществляется по следующему правилу:
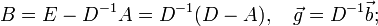
где в принятых обозначениях D означает матрицу, у которой на главной диагонали стоят соответствующие элементы матрицы A,
а все остальные нули; тогда как матрицы U и L содержат верхнюю и нижнюю треугольные части A,
на главной диагонали которых нули, E — единичная матрица.
Тогда процедура нахождения решения имеет вид:
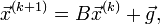 где k счётчик итерации.
Условие окончания итерационного процесса при достижении заданной точности имеет вид:
где k счётчик итерации.
Условие окончания итерационного процесса при достижении заданной точности имеет вид:
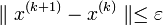 . .
- Описание схемы параллельной реализации
Определим параллельную схему для реализации алгоритма решения поставленной задачи.
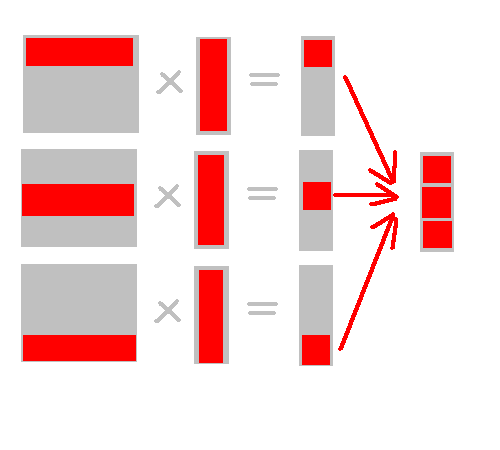
На каждой k-ой итерации мы вычисляем k-ое приближение вектора решений.
Компоненты вычисляемого вектора независимы между собой и
их вычиление зависит только от компонент вектора, полученного не предыдущей итерации.
Поэтому каждый узел будет параллельно вычислять свой компонент результирующего вектора (или несколько компонент).
Затем все результаты вычислений будут пересылаться каждому узлу, так как вектор полученный на предыдущей итерации
нужен для вычисления следующего приближения.
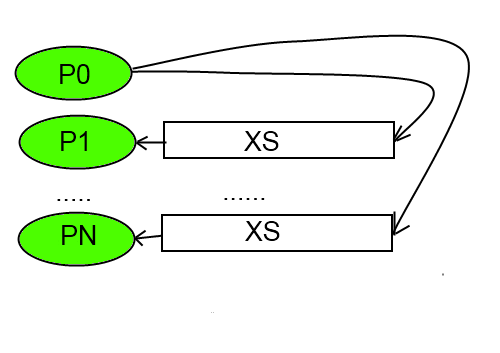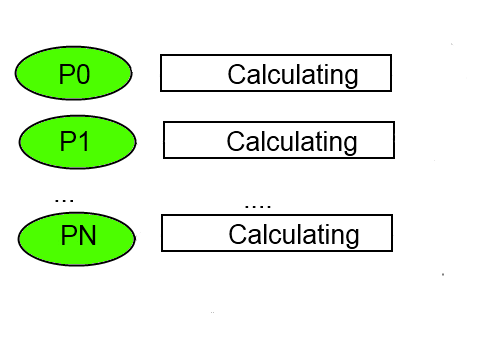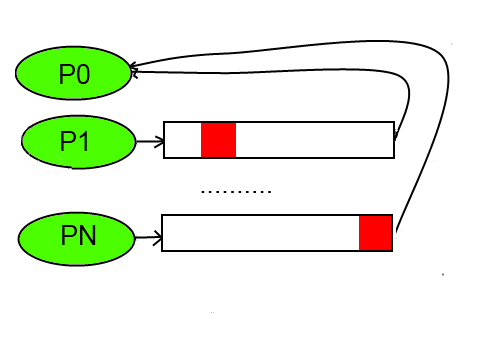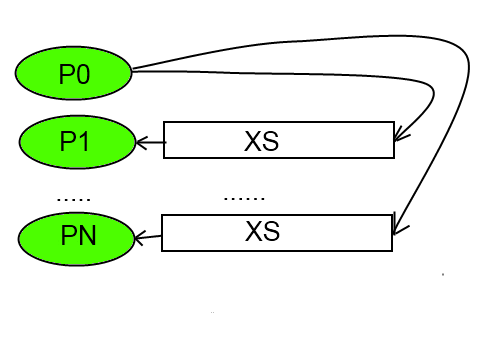
- Динамическая визуализация
- Теоретический анализ эффективности
Время, затраченное на последовательное выполнение алгоритма, выражается следующей формулой:
T = m * (2*n^2 - n), где m – число выполненных итераций, а n – число уравнений.
Время, затраченное на параллельное выполнение алгоритма на p процессорах (без учета времени на передачу данных) выражается формулой:
T(p) = m/p * (2*n^2 - n)
Тогда ускорение равно:
S = T(1) / T(p) = p
Эффективность: E = T1 / p*Tp = 1
Определим затраты времени на передачу данных. Для этого используем модель Хокни.
Первоначальная рассылка данных требует следующее время:
Tcomm1 = (p-1) * (4*alfa + (n^2 / p + n) / betta)
, где alfa - латентность, betta - пропускная способность сети.
Передача данных, выполняемая в итерационном процессе, затрачивает следующее время:
Tcomm2 = m * (p-1) * (3*alfa + (n / p + n) / betta)
, где m - количество выполненных итераций.
В итоге общее время передачи данных выражается формулой:
Tcomm = (p-1) * (4*alfa + (n^2 / p + n) / betta) + k * (p-1) * (3*alfa + (n / p + n) / betta)
Это время зависит от числа итераций. Как правило, их количество меньше числа уравнений n.
Значит время на передачу данных можно оценить величиной:
Tcomm = O(n^2)
В свою очередь и ко времени выполнения алгоритма применима та же оценка:
T = O(n^2)
Если число итераций будет сравнимо с n, то для времени выполнения алгоритма будет справедлива уже другая оценка:
T = O(n^3)
- Результаты проведенных экспериментов
Характеристики используемой для рассчетов машины:
Intel Core-i5-2410M CPU @ 2.3GHz, 4 GB RAM.
Время работы алгортимов и ускорения представлены в таблице:
|
Матрица
|
Число итераций
|
Последовательные (в 1 процесс)
|
Параллельные в 2 процесса
|
Ускорение при 2 процессаx
|
Параллельные в 4 процесса
|
Ускорение при 4 процессаx
|
|
50x50
|
366
|
0,37
|
0,19
|
0,18
|
0,17
|
0,2
|
|
100x100
|
744
|
3,1
|
1,5
|
1,6
|
1,4
|
1,7
|
|
|



